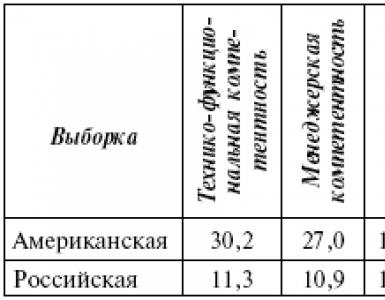
Типы процедур кластер-анализа. И.А

При большом количестве наблюдений иерархические методы кластерного анализа не пригодны. В таких случаях используют неиерархические методы, основанные на разделении, которые представляют собой итеративные методы дробления исходной совокупности. В процессе деления новые кластеры формируются до тех пор, пока не будет выполнено правило остановки.

Такая неиерархическая кластеризация состоит в разделении набора данных на определенное количество отдельных кластеров. Существует два подхода. Первый заключается в определении границ кластеров как наиболее плотных участков в многомерном пространстве исходных данных, т.е. определение кластера там, где имеется большое "сгущение точек". Второй подход заключается в минимизации меры различия объектов

Алгоритм k-средних (k-means)

Наиболее распространен среди неиерархических методов алгоритм k-средних, также называемый быстрым кластерным анализом. Полное описание алгоритма можно найти в работе Хартигана и Вонга (Hartigan and Wong, 1978). В отличие от иерархических методов, которые не требуют предварительных предположений относительно числа кластеров, для возможности использования этого метода необходимо иметь гипотезу о наиболее вероятном количестве кластеров.

Алгоритм k-средних строит k кластеров, расположенных на возможно больших расстояниях друг от друга. Основной тип задач, которые решает алгоритм k-средних, - наличие предположений (гипотез) относительно числа кластеров, при этом они должны быть различны настолько, насколько это возможно. Выбор числа k может базироваться на результатах предшествующих исследований, теоретических соображениях или интуиции.

Общая идея алгоритма: заданное фиксированное число k кластеров наблюдения сопоставляются кластерам так, что средние в кластере (для всех переменных) максимально возможно отличаются друг от друга.

Описание алгоритма

1. Первоначальное распределение объектов по кластерам. Выбирается число k, и на первом шаге эти точки считаются "центрами" кластеров. Каждому кластеру соответствует один центр.
   Выбор начальных центроидов может осуществляться следующим образом:
   - выбор k-наблюдений для максимизации начального расстояния;
   - случайный выбор k-наблюдений;
   - выбор первых k-наблюдений.
   В результате каждый объект назначен определенному кластеру.
2. Итеративный процесс. Вычисляются центры кластеров, которыми затем и далее считаются покоординатные средние кластеров. Объекты опять перераспределяются.
   Процесс вычисления центров и перераспределения объектов продолжается до тех пор, пока не выполнено одно из условий:
   - кластерные центры стабилизировались, т.е. все наблюдения принадлежат кластеру, которому принадлежали до текущей итерации;
   - число итераций равно максимальному числу итераций.

На рис. 14.1 приведен пример работы алгоритма k-средних для k, равного двум.

Рисунок 1 - Пример работы алгоритма k-средних (k=2)

Выбор числа кластеров является сложным вопросом. Если нет предположений относительно этого числа, рекомендуют создать 2 кластера, затем 3, 4, 5 и т.д., сравнивая полученные результаты.

Проверка качества кластеризации

После получений результатов кластерного анализа методом k-средних следует проверить правильность кластеризации (т.е. оценить, насколько кластеры отличаются друг от друга). Для этого рассчитываются средние значения для каждого кластера. При хорошей кластеризации должны быть получены сильно отличающиеся средние для всех измерений или хотя бы большей их части.

Достоинства алгоритма k-средних:

1. простота использования;
2. быстрота использования;
3. понятность и прозрачность алгоритма.

Недостатки алгоритма k-средних:

1. алгоритм слишком чувствителен к выбросам, которые могут искажать среднее. Возможным решением этой проблемы является использование модификации алгоритма - алгоритм k-медианы;
2. алгоритм может медленно работать на больших базах данных. Возможным решением данной проблемы является использование выборки данных.

Алгоритм PAM (partitioning around Medoids)

PAM является модификацией алгоритма k-средних, алгоритмом k-медианы (k-medoids).

Алгоритм менее чувствителен к шумам и выбросам данных, чем алгоритм k-means, поскольку медиана меньше подвержена влияниям выбросов.

PAM эффективен для небольших баз данных, но его не следует использовать для больших наборов данных. Предварительное сокращение размерности

Рассмотрим пример. Есть база данных клиентов фирмы, которых следует разбить на однородные группы. Каждый клиент описывается при помощи 25 переменных. Использование такого большого числа переменных приводит к выделению кластеров нечеткой структуры. В результате аналитику достаточно сложно интерпретировать полученные кластеры.

Более понятные и прозрачные результаты кластеризации могут быть получены, если вместо множества исходных переменных использовать некие обобщенные переменные или критерии, содержащие в сжатом виде информацию о связях между переменными. Т.е. возникает задача понижения размерности данных. Она может решаться при помощи различных методов; один из наиболее распространенных - факторный анализ. Остановимся на нем более подробно.

Факторный анализ

Факторный анализ - это метод, применяемый для изучения взаимосвязей между значениями переменных.

Вообще, факторный анализ преследует две цели:

1. сокращение числа переменных;
2. классификацию переменных - определение структуры взаимосвязей между переменными.

Соответственно, факторный анализ может использоваться для решения задач сокращения размерности данных или для решения задач классификации.

Критерии или главные факторы, выделенные в результате факторного анализа, содержат в сжатом виде информацию о существующих связях между переменными. Эта информация позволяет получить лучшие результаты кластеризации и лучше объяснить семантику кластеров. Самим факторам может быть сообщен определенный смысл.

При помощи факторного анализа большое число переменных сводится к меньшему числу независимых влияющих величин, которые называются факторами.

Фактор в "сжатом" виде содержит информацию о нескольких переменных. В один фактор объединяются переменные, которые сильно коррелируют между собой. В результате факторного анализа отыскиваются такие комплексные факторы, которые как можно более полно объясняют связи между рассматриваемыми переменными.

На первом шаге факторного анализа осуществляется стандартизация значений переменных, необходимость которой была рассмотрена в предыдущей лекции.

Факторный анализ опирается на гипотезу о том, что анализируемые переменные являются косвенными проявлениями сравнительно небольшого числа неких скрытых факторов.

Факторный анализ - это совокупность методов, ориентированных на выявление и анализ скрытых зависимостей между наблюдаемыми переменными. Скрытые зависимости также называют латентными.

Один из методов факторного анализа - метод главных компонент - основан на предположении о независимости факторов друг от друга.

Итеративная кластеризация в SPSS Обычно в статистических пакетах реализован широкий арсенал методов, что позволяет сначала провести сокращение размерности набора данных (например, при помощи факторного анализа), а затем уже собственно кластеризацию (например, методом быстрого кластерного анализа). Рассмотрим этот вариант проведения кластеризации в пакете SPSS.
Для сокращения размерности исходных данных воспользуемся факторным анализом. Для этого выберем в меню: Analyze (Анализ)/Data Reduction (Преобразование данных)/Factor (Факторный анализ):
При помощи кнопки Extraction:(Отбор) следует выбрать метод отбора. Мы оставим выбранный по умолчанию анализ главных компонентов, который упоминался выше. Также следует выбрать метод вращения - выберем один из наиболее популярных - метод варимакса. Для сохранения значений факторов в виде переменных в закладке "Значения" необходимо поставить отметку "Save as variables" (Сохранить как переменные).

В результате этой процедуры пользователь получает отчет "Объясненная суммарная дисперсия", по которой видно число отобранных факторов - это те компоненты, собственные значения которых превосходят единицу.

Полученные значения факторов, которым обычно присваиваются названия fact1_1, fact1_2 и т.д., используем для проведения кластерного анализа методом k-средних. Для проведения быстрого кластерного анализа выберем в меню:

Analyze (Анализ)/Classify(Классифицировать)/K-Means Cluster: (Кластерный анализ методом k-средних).

В диалоговом окне K Means Cluster Analysis (Кластерный анализ методом k-средних) необходимо поместить факторные переменные fact1_1, fact1_2 и т.д. в поле тестируемых переменных. Здесь же необходимо указать количество кластеров и количество итераций.

В результате этой процедуры получаем отчет с выводом значений центров сформированных кластеров, количестве наблюдений в каждом кластере, а также с дополнительной информацией, заданной пользователем.

Таким образом, алгоритм k-средних делит совокупность исходных данных на заданное количество кластеров. Для возможности визуализации полученных результатов следует воспользоваться одним из графиков, например, диаграммой рассеивания. Однако традиционная визуализация возможна для ограниченного количества измерений, ибо, как известно, человек может воспринимать только трехмерное пространство. Поэтому, если мы анализируем более трех переменных, следует использовать специальные многомерные методы представления информации, о них будет рассказано в одной из последующих лекций курса.

Итеративные методы кластеризации различаются выбором следующих параметров:

1. начальной точки;
2. правилом формирования новых кластеров;
3. правилом остановки.

Выбор метода кластеризации зависит от количества данных и от того, есть ли необходимость работать одновременно с несколькими типами данных.

В пакете SPSS, например, при необходимости работы как с количественными (например, доход), так и с категориальными (например, семейное положение) переменными, а также если объем данных достаточно велик, используется метод Двухэтапного кластерного анализа, который представляет собой масштабируемую процедуру кластерного анализа, позволяющую работать с данными различных типов. Для этого на первом этапе работы записи предварительно кластеризуются в большое количество суб-кластеров. На втором этапе полученные суб-кластеры группируются в необходимое количество. Если это количество неизвестно, процедура сама автоматически определяет его. При помощи этой процедуры банковский работник может, например,выделять группы людей, одновременно используя такие показатели как возраст, пол и уровень дохода. Полученные результаты позволяют определить клиентов, входящих в группы риска невозврата кредита.

В общем случае все этапы кластерного анализа взаимосвязаны, и решения, принятые на одном из них, определяют действия на последующих этапах.

Аналитику следует решить, использовать ли все наблюдения либо же исключить некоторые данные или выборки из набора данных.

Выбор метрики и метода стандартизации исходных данных.

Определение количества кластеров (для итеративного кластерного анализа).

Определение метода кластеризации (правила объединения или связи).

По мнению многих специалистов, выбор метода кластеризации является решающим при определении формы и специфики кластеров.

Анализ результатов кластеризации. Этот этап подразумевает решение таких вопросов: не является ли полученное разбиение на кластеры случайным; является ли разбиение надежным и стабильным на подвыборках данных; существует ли взаимосвязь между результатами кластеризации и переменными, которые не участвовали в процессе кластеризации; можно ли интерпретировать полученные результаты кластеризации.

Проверка результатов кластеризации. Результаты кластеризации также должны быть проверены формальными и неформальными методами. Формальные методы зависят от того метода, который использовался для кластеризации. Неформальные включают следующие процедуры проверки качества кластеризации:

1. анализ результатов кластеризации, полученных на определенных выборках набора данных;
2. кросс-проверка;
3. проведение кластеризации при изменении порядка наблюдений в наборе данных;
4. проведение кластеризации при удалении некоторых наблюдений;
5. проведение кластеризации на небольших выборках.

Один из вариантов проверки качества кластеризации - использование нескольких методов и сравнение полученных результатов. Отсутствие подобия не будет означать некорректность результатов, но присутствие похожих групп считается признаком качественной кластеризации.

Сложности и проблемы, которые могут возникнуть при применении кластерного анализа

Как и любые другие методы, методы кластерного анализа имеют определенные слабые стороны, т.е. некоторые сложности, проблемы и ограничения.

При проведении кластерного анализа следует учитывать, что результаты кластеризации зависят от критериев разбиения совокупности исходных данных. При понижении размерности данных могут возникнуть определенные искажения, за счет обобщений могут потеряться некоторые индивидуальные характеристики объектов.

Существует ряд сложностей, которые следует продумать перед проведением кластеризации.

1. Сложность выбора характеристик, на основе которых проводится кластеризация. Необдуманный выбор приводит к неадекватному разбиению на кластеры и, как следствие, - к неверному решению задачи.
2. Сложность выбора метода кластеризации. Этот выбор требует неплохого знания методов и предпосылок их использования. Чтобы проверить эффективность конкретного метода в определенной предметной области, целесообразно применить следующую процедуру: рассматривают несколько априори различных между собой групп и перемешивают их представителей между собой случайным образом. Далее проводится кластеризация для восстановления исходного разбиения на кластеры. Доля совпадений объектов в выявленных и исходных группах является показателем эффективности работы метода.
3. Проблема выбора числа кластеров. Если нет никаких сведений относительно возможного числа кластеров, необходимо провести ряд экспериментов и, в результате перебора различного числа кластеров, выбрать оптимальное их число.
4. Проблема интерпретации результатов кластеризации. Форма кластеров в большинстве случаев определяется выбором метода объединения. Однако следует учитывать, что конкретные методы стремятся создавать кластеры определенных форм, даже если в исследуемом наборе данных кластеров на самом деле нет.

Сравнительный анализ иерархических и неиерархических методов кластеризации

Перед проведением кластеризации у аналитика может возникнуть вопрос, какой группе методов кластерного анализа отдать предпочтение. Выбирая между иерархическими и неиерархическими методами, необходимо учитывать следующие их особенности.

Неиерархические методы выявляют более высокую устойчивость по отношению к шумам и выбросам, некорректному выбору метрики, включению незначимых переменных в набор, участвующий в кластеризации. Ценой, которую приходится платить за эти достоинства метода, является слово "априори". Аналитик должен заранее определить количество кластеров, количество итераций или правило остановки, а также некоторые другие параметры кластеризации. Это особенно сложно начинающим специалистам.

Если нет предположений относительно числа кластеров, рекомендуют использовать иерархические алгоритмы. Однако если объем выборки не позволяет это сделать, возможный путь - проведение ряда экспериментов с различным количеством кластеров, например, начать разбиение совокупности данных с двух групп и, постепенно увеличивая их количество, сравнивать результаты. За счет такого "варьирования" результатов достигается достаточно большая гибкость кластеризации.

Иерархические методы, в отличие от неиерархических, отказываются от определения числа кластеров, а строят полное дерево вложенных кластеров.

Сложности иерархических методов кластеризации: ограничение объема набора данных; выбор меры близости; негибкость полученных классификаций.

Преимущество этой группы методов в сравнении с неиерархическими методами - их наглядность и возможность получить детальное представление о структуре данных.

При использовании иерархических методов существует возможность достаточно легко идентифицировать выбросы в наборе данных и, в результате, повысить качество данных. Эта процедура лежит в основе двухшагового алгоритма кластеризации. Такой набор данных в дальнейшем может быть использован для проведения неиерархической кластеризации.

Существует еще одни аспект, о котором уже упоминалось в этой лекции. Это вопрос кластеризации всей совокупности данных или же ее выборки. Названный аспект существенен для обеих рассматриваемых групп методов, однако он более критичен для иерархических методов. Иерархические методы не могут работать с большими наборами данных, а использование некоторой выборки, т.е. части данных, могло бы позволить применять эти методы.

Результаты кластеризации могут не иметь достаточного статистического обоснования. С другой стороны, при решении задач кластеризации допустима нестатистическая интерпретация полученных результатов, а также достаточно большое разнообразие вариантов понятия кластера. Такая нестатистическая интерпретация дает возможность аналитику получить удовлетворяющие его результаты кластеризации, что при использовании других методов часто бывает затруднительным.

Новые алгоритмы и некоторые модификации алгоритмов кластерного анализа

Методы, которые мы рассмотрели в этой и предыдущей лекциях, являются "классикой" кластерного анализа. До последнего времени основным критерием, по которому оценивался алгоритм кластеризации, было качество кластеризации: полагалось, чтобы весь набор данных умещался в оперативной памяти.

Однако сейчас, в связи с появлением сверхбольших баз данных, появились новые требования, которым должен удовлетворять алгоритм кластеризации. Основное из них, как уже упоминалось в предыдущих лекциях, - это масштабируемость алгоритма.

Отметим также другие свойства, которым должен удовлетворять алгоритм кластеризации: независимость результатов от порядка входных данных; независимость параметров алгоритма от входных данных.

В последнее время ведутся активные разработки новых алгоритмов кластеризации, способных обрабатывать сверхбольшие базы данных. В них основное внимание уделяется масштабируемости. К таким алгоритмам относятся обобщенное представление кластеров (summarized cluster representation), а также выборка и использование структур данных, поддерживаемых нижележащими СУБД .

Разработаны алгоритмы, в которых методы иерархической кластеризации интегрированы с другими методами. К таким алгоритмам относятся: BIRCH, CURE, CHAMELEON, ROCK.

Алгоритм BIRCH (Balanced Iterative Reducing and Clustering using Hierarchies)

Алгоритм предложен Тьян Зангом и его коллегами .

Благодаря обобщенным представлениям кластеров, скорость кластеризации увеличивается, алгоритм при этом обладает большим масштабированием.

В этом алгоритме реализован двухэтапный процесс кластеризации.

В ходе первого этапа формируется предварительный набор кластеров. На втором этапе к выявленным кластерам применяются другие алгоритмы кластеризации - пригодные для работы в оперативной памяти.

В приведена следующая аналогия, описывающая этот алгоритм. Если каждый элемент данных представить себе как бусину, лежащую на поверхности стола, то кластеры бусин можно "заменить" теннисными шариками и перейти к более детальному изучению кластеров теннисных шариков. Число бусин может оказаться достаточно велико, однако диаметр теннисных шариков можно подобрать таким образом, чтобы на втором этапе можно было, применив традиционные алгоритмы кластеризации, определить действительную сложную форму кластеров.

Алгоритм WaveCluster

WaveCluster представляет собой алгоритм кластеризации на основе волновых преобразований . В начале работы алгоритма данные обобщаются путем наложения на пространство данных многомерной решетки. На дальнейших шагах алгоритма анализируются не отдельные точки, а обобщенные характеристики точек, попавших в одну ячейку решетки. В результате такого обобщения необходимая информация умещается в оперативной памяти. На последующих шагах для определения кластеров алгоритм применяет волновое преобразование к обобщенным данным.

Главные особенности WaveCluster:

1. сложность реализации;
2. алгоритм может обнаруживать кластеры произвольных форм;
3. алгоритм не чувствителен к шумам;
4. алгоритм применим только к данным низкой размерности.

Алгоритм CLARA (Clustering LARge Applications)

Алгоритм CLARA был разработан Kaufmann и Rousseeuw в 1990 году для кластеризации данных в больших базах данных. Данный алгоритм строится в статистических аналитических пакетах, например, таких как S+.

Изложим кратко суть алгоритма. Алгоритм CLARA извлекает множество образцов из базы данных. Кластеризация применяется к каждому из образцов, на выходе алгоритма предлагается лучшая кластеризация.

Для больших баз данных этот алгоритм эффективнее, чем алгоритм PAM. Эффективность алгоритма зависит от выбранного в качестве образца набора данных. Хорошая кластеризация на выбранном наборе может не дать хорошую кластеризацию на всем множестве данных.

Алгоритмы Clarans, CURE, DBScan

Алгоритм Clarans (Clustering Large Applications based upon RANdomized Search) формулирует задачу кластеризации как случайный поиск в графе. В результате работы этого алгоритма совокупность узлов графа представляет собой разбиение множества данных на число кластеров, определенное пользователем. "Качество" полученных кластеров определяется при помощи критериальной функции. Алгоритм Clarans сортирует все возможные разбиения множества данных в поисках приемлемого решения. Поиск решения останавливается в том узле, где достигается минимум среди предопределенного числа локальных минимумов.

Среди новых масштабируемых алгоритмов также можно отметить алгоритм CURE - алгоритм иерархической кластеризации, и алгоритм DBScan , где понятие кластера формулируется с использованием концепции плотности (density).

Основным недостатком алгоритмов BIRCH, Clarans, CURE, DBScan является то обстоятельство, что они требуют задания некоторых порогов плотности точек, а это не всегда приемлемо. Эти ограничения обусловлены тем, что описанные алгоритмы ориентированы на сверхбольшие базы данных и не могут пользоваться большими вычислительными ресурсами .

Над масштабируемыми методами сейчас активно работают многие исследователи, основная задача которых - преодолеть недостатки алгоритмов, существующих на сегодняшний день.

Кластерный анализ (КлА)– это совокупность методов многомерной классификации, целью которой является образование групп (кластеров) схожих между собой объектов. В отличие от традиционных группировок, рассматриваемых в общей теории статистики, КлА приводит к разбиению на группы с учетом всех группировочных признаков одновременно.

Методы КлА позволяют решать следующие задачи:

— проведение классификации объектов с учетом множества признаков;

— проверка выдвигаемых предположений о наличии некоторой структуры в изучаемой совокупности объектов, т.е. поиск существующей структуры;

— построение новых классификаций для слабо изученных явлений, когда необходимо установить наличие связей внутри совокупности и попытаться привнести в нее структуру.

Для записи формализованных алгоритмов КлА используются следующие условные обозначения:

– совокупность объектов наблюдения;

– i-е наблюдение в m-мерном пространстве признаков ();

– расстояние между -м и -м объектами;

– нормированные значения исходных переменных;

– матрица расстояний между объектами.

Для реализации любого метода КлА необходимо ввести понятие «сходство объектов». Причем в процессе классификации в каждый кластер должны попадать объекты, имеющие наибольшее сходство друг с другом с точки зрения наблюдаемых переменных.

Для количественной оценки сходства вводится понятие метрики. Каждый объект описывается -признаками и представлен как точка в -мерном пространстве. Сходство или различие между классифицируемыми объектами устанавливается в зависимости от метрического расстояния между ними. Как правило, используются следующие меры расстояния между объектами:

— евклидово расстояние ;

— взвешенное евклидово расстояние ;

— расстояние city-block ;

— расстояние Махаланобиса ,

где – расстояние между -ым и -ым объектами;

, – значения -переменной и соответственно у -го и -го объектов;

, – векторы значений переменных у -го и -го объектов;

– общая ковариационная матрица;

– вес, приписываемый -й переменной.

Все методы КлА можно разделить на две группы: иерархические (агломеративные и дивизимные) и итеративные (метод -cpeдних, метод поиска сгущений).

Иерархический кластерный анализ. Из всех методов кластерного анализа наиболее распространенными является агломеративный алгоритм классификации. Сущность аглогритма заключается в том, что на первом шаге каждый объект выборки рассматривается как отдельный кластер. Процесс объединения кластеров происходит последовательно: на основании матрицы расстояний или матрицы сходства объединяются наиболее близкие объекты. Если матрица расстояний первоначально имеет размерность (), то полностью процесс объединения завершается за () шагов. В итоге все объекты будут объединены в один кластер.

Последовательность объединения может быть представлена в виде дендрограммы, представленной на рисунке 3.1. Дендрограмма показывает, что на первом шаге объединены в один кластер второй и третий объекты при расстоянии между ними 0,15. На втором шаге к ним присоединился первый объект. Расстояние от первого объекта до кластера, содержащего второй и третий объекты, 0,3 и т.д.

Множество методов иерархического кластерного анализа отличаются алгоритмами объединения (сходства), из которых наиболее распространенными являются: метод одиночной связи, метод полных связей, метод средней связи, метод Уорда.

Метод полных связей – включение нового объекта в кластер происходит только в том случае, если сходство между всеми объектами не меньше некоторого заданного уровня сходства (рисунок 1.3).

б)

Метод средней связи – при включении нового объекта в уже существующий кластер вычисляется среднее значение меры сходства, которое затем сравнивается с заданным пороговым уровнем. Если речь идет об объединении двух кластеров, то вычисляют меру сходства между их центрами и сравнивают ее с заданным пороговым значением. Рассмотрим геометрический пример с двумя кластерами (рисунок 1.4).

Рисунок 1.4. Объединение двух кластеров по методу средней связи:

Если мера сходства между центрами кластеров () будет не меньше заданного уровня, то кластеры и будут объединены в один.

Метод Уорда – на первом шаге каждый кластер состоит из одного объекта. Первоначально объединяются два ближайших кластера. Для них определяются средние значения каждого признака и рассчитывается сумма квадратов отклонений

, (1.1)

где – номер кластера, – номер объекта, – номер признака; – количество признаков, характеризующих каждый объект; – количество объектов в -мкластере.

В дальнейшем на каждом шаге работы алгоритма объединяются те объекты или кластеры, которые дают наименьшее приращение величины .

Метод Уорда приводит к образованию кластеров приблизительно равных размеров с минимальной внутрикластерной вариацией.

Алгоритм иерархического кластерного анализа можно представить в виде последовательности процедур:

— нормирование исходных значений переменных;

— расчет матрицы расстояний или матрицы мер сходства;

— определение пары самых близких объектов (кластеров) и их объединение по выбранному алгоритму;

— повторение первых трех процедур до тех пор, пока все объекты не будут объединены в один кластер.

Мера сходства для объединения двух кластеров определяется следующими методами:

— метод «ближайшего соседа» – степень сходства между кластерами оценивается по степени сходства между наиболее схожими (ближайшими) объектами этих кластеров;

— метод «дальнего соседа» – степень сходства оценивается по степени сходства между наиболее отдаленными (несхожими) объектами кластеров;

— метод средней связи – степень сходства оценивается как средняя величина степеней сходства между объектами кластеров;

— метод медианной связи – расстояние между любым кластером S и новым кластером, который получился в результате объединения кластеров р и q, определяется как расстояние от центра кластера S до середины отрезка, соединяющего центры кластеров р и q.

Метод поиска сгущений. Одним из итеративных методов классификации является алгоритм поиска сгущений. Суть итеративного алгоритма данного метода заключается в применении гиперсферы заданного радиуса, которая перемещается в пространстве классификационных признаков с целью поиска локальных сгущений объектов.

Метод поиска сгущений требует, прежде всего, вычисления матрицы расстояний (или матрицы мер сходства) между объектами и выбора первоначального центра сферы. Обычно на первом шаге центром сферы служит объект (точка), в ближайшей окрестности которого расположено наибольшее число соседей. На основе заданного радиуса сферы (R) определяется совокупность точек, попавших внутрь этой сферы, и для них вычисляются координаты центра (вектор средних значений признаков).

Когда очередной пересчет координат центра сферы приводит к такому же результату, как и на предыдущем шаге, перемещение сферы прекращается, а точки, попавшие в нее, образуют кластер, и из дальнейшего процесса кластеризации исключаются. Перечисленные процедуры повторяются для всех оставшихся точек. Работа алгоритма завершается за конечное число шагов, и все точки оказываются распределенными по кластерам. Число образовавшихся кластеров заранее неизвестно и сильно зависит от радиуса сферы.

Для оценки устойчивости полученного разбиения целесообразно повторить процесс кластеризации несколько раз для различных значений радиуса сферы, изменяя каждый раз радиус на небольшую величину.

Существуют несколько способов выбора радиуса сферы. Если – расстояние между -м и -м объектами, то в качестве нижней границы радиуса ()выбирают , а верхняя граница радиуса может быть определена как .

Если начинать работу алгоритма с величины и при каждом его повторении изменять на небольшую величину, то можно выявить значения радиусов, которые приводят к образованию одного и того же числа кластеров, т.е. к устойчивому разбиению.

Пример 1. На основании приведенных данных таблицы 1.1 необходимо провести классификацию пяти предприятий при помощи иерархического агломеративного кластерного анализа.

Таблица 1.1

Здесь: – среднегодовая стоимость основных производственных фондов, млрд. р.; – материальные затраты на один рубль произведенной продукции, коп.; – объем произведенной продукции, млрд. р.

Решение. Перед тем как вычислять матрицу расстояний, нормируем исходные данные по формуле

Матрица значений нормированных переменных будет иметь вид

.

Классификацию проведем при помощи иерархического агломеративного метода. Для построения матрицы расстояний воспользуемся евклидовым расстоянием. Тогда, например, расстояние между первым и вторым объектами будет

Матрица расстояний характеризует расстояния между объектами, каждый из которых, на первом шаге представляет собой отдельный кластер

.

Как видно из матрицы , наиболее близкими являются объекты и . Объединим их в один кластер и присвоим ему номер . Пересчитаем расстояния всех оставшихся объектов (кластеров) до кластера получим новую матрицу расстояний

.

В матрице расстояния между кластерами определены по алгоритму «дальнего соседа». Тогда расстояние между объектом и кластером равно

В матрице опять находим самые близкие кластеры. Это будут и , . Следовательно, на этом шаге объединяем и кластеры; получим новый кластер, содержащий объекты , . Присвоим ему номер . Теперь имеем три кластера {1,3}, {2,5}, {4}.

.

Судя по матрице ,на следующем шаге объединяем кластеры и , в один кластер и присвоим ему номер . Теперь имеем только два кластера:

.

И, наконец, на последнем шаге объединим кластеры и на расстоянии 3,861.

Представим результаты классификации в виде дендрограммы (рисунок 1.5). Дендрограмма свидетельствует о том, что кластер более однороден по составу входящих объектов, так как в нем объединение происходило при меньших расстояниях, чем в кластере .

Рисунок 3.5.Дендрограмма кластеризации пяти объектов

Пример 2. На основании данных, приведенных ниже, проведите классификацию магазинов по трем признакам: – площадь торгового зала, м2 , – товарооборот на одного продавца, ден. ед., – уровень рентабельности, %.

Номермагазина				Номермагазина

Для классификации магазинов используйте метод поиска сгущений (необходимо выделить первый кластер).

Решение. 1. Рассчитаем расстояния между объектами по евклидовой метрике

,

где , – стандартизированные значения исходных переменных соответственно у -го и -го объектов; т – число признаков.

.

2. На основе матрицы Z рассчитаем квадратную симметричную матрицу расстояний между объектами ().

Анализ матрицы расстояний помогает определить положение первоначального центра сферы и выбрать радиус сферы.

В данном примере большинство «маленьких» расстояний находятся в первой строке, т.е. у первого объекта достаточно много «близких» соседей. Следовательно, первый объект можно взять в качестве центра сферы.

3. Зададим радиус сферы . В этом случае в сферу попадают объекты, расстояние которых до первого объекта меньше 2.

Одним из итеративных методов классификации, не требующих задания числа кластеров, является метод поиска сгущений. Метод требует вычисления матрицы расстояний, затем выбирается объект, который является первоначальным центром первого кластера. Выбор такого объекта может быть произвольным, а может основываться на предварительном анализе точек и их окрестностей.

Выбранная точка принимается за центр гиперсферы заданного радиуса R. Определяется совокупность точек, попавших внутрь этой сферы, и для них вычисляются координаты центра (вектор средних значений признаков). Далее рассматривается гиперсфера такого же радиуса, но с новым центром, и для совокупности попавших в нее точек опять рассчитывается вектор средних значений, который принимается за новый центр сферы и так далее. Когда очередной пересчет координат центра сферы приводит к такому же результату, как на предыдущем шаге, перемещение сферы прекращается, а точки, попавшие в нее, образуют кластер и из дальнейшего процесса кластеризации исключаются. Для всех оставшихся точек процедуры повторяются .

Таким образом, неиерархических методов больше, хотя работают они на одних и тех же принципах. По сути, они представляют собой итеративные методы дробления исходной совокупности. В процессе деления формируются новые кластеры, и так до тех пор, пока не будет выполнено правило остановки. Между собой методы различаются выбором начальной точки, правило формирования новых кластеров и правилом остановки. Чаще всего используется алгоритм К-средних .

Заключение

Кластерный анализ - метод группировки объектов в классы на основании экспериментальных данных о свойствах объектов.

При этом используется кластерная модель представления объектов - объекты со схожими свойствами относятся к одному классу.

Кластерный анализ включает в себя набор различных алгоритмов классификации (в качестве примера метода кластерного анализа можно привести метод дендрограмм).

При этом, как правило, количество классов и принципы разделения на классы определяются заранее исходя из общей информации о наборе объектов и целей кластерного анализа.

Методы кластерного анализа дополняется методами дискриминантного анализа, которые позволяют определить границы между кластерами и использовать их для решения задач анализа и классификации данных.

Результаты кластер-анализа чаще всего представляются графически, в виде дендрограммы («дерева»), показывающей порядок объединения объектов в кластеры. Интерпретация кластерной структуры, которая во многих случаях начинается с определения числа кластеров, является творческой задачей. Для того, чтобы она могла быть эффективно решена, исследователь должен располагать достаточной информацией о кластеризуемых объектах. При кластеризации «с обучением» результаты могут быть представлены в виде списков объектов, отнесенных к каждому классу.

Основными преимуществами кластер-анализа являются отсутствие ограничений на распределение переменных, используемых в анализе; возможность классификации (кластеризации) даже в тех случаях, когда нет никакой априорной информации о количестве и характере классов; универсальность (кластерный анализ может применяться не только к совокупностям объектов, но также к наборам переменных или любых других единиц анализа).

Перечислим недостатки кластерного анализа:

Как и факторный анализ, он может давать неустойчивые кластеры. Повторите исследование на других людях и сравните результаты классификации. Скорее всего, они будут отличаться. На сколько - вопрос качества самого исследования.

Он реализует индуктивный метод исследования от частного к общему, что чревато антинаучными выводами. В идеале выборка для классификации должна быть очень большая, неоднородная, желательно подобранная методом стратификации или рандомизации. Наука движется по пути проверки гипотез, поэтому не нужно злоупотреблять кластерным анализом. Лучше всего использовать его для проверки гипотезы о наличии каких-либо типов, а не создавать классификацию на голом месте.

Как и любой метод многомерного шкалирования, кластерный анализ имеет множество особенностей, связанных с внутренними методами. Каков критерий объединения людей в кластеры, метод поиска различий, количество шагов до завершения алгоритма в методе к-средних и т.д. поэтому результаты могут меняться, хоть и несущественно, в зависимости от «настроек» процедуры.

Выделяют две группы методов кластерного анализа : иерархические и неиерархические.

Основными методами иерархического кластерного анализа являются метод ближнего соседа, метод полной связи, метод средней связи и метод Варда. Наиболее универсальным является последний.

Неиерархических методов больше, хотя работают они на одних и тех же принципах. По сути, они представляют собой итеративные методы дробления исходной совокупности. В процессе деления формируются новые кластеры, и так до тех пор, пока не будет выполнено правило остановки. Между собой методы различаются выбором начальной точки, правило формирования новых кластеров и правилом остановки. Чаще всего используется алгоритм К-средних . Он подразумевает, что аналитик заранее фиксирует количество кластеров в результирующем разбиении.

Говоря о выборе конкретного метода кластеризации, еще раз подчеркнем, что этот процесс требует от аналитика хорошего знакомства с природой и предпосылками методов, в противном случае полученные результаты будут похожи на «среднюю температуру по больнице». Для того чтобы убедиться в том, что выбранный метод действительно эффективен в данной области, как правило, применяют следующую процедуру:

Рассматривают несколько априори различных между собой групп и перемешивают их представителей между собой случайным образом. Затем проводят процедуру кластеризации с целью восстановить исходное разбиение на группы. Показателем эффективности работы метода будет доля совпадений объектов в выявленных и исходных группах.

Выбирая между иерархическими и неиерархическими методами, следует обратить внимание на следующие моменты:

Неиерархические методы обнаруживают более высокую устойчивость по отношению к выбросам, неверному выбору метрики, включению незначимых переменных в базу для кластеризации и пр. Но платой за это является слово «априори». Исследователь должен заранее фиксировать результирующее количество кластеров, правило остановки и, если на то есть основания, начальный центр кластера. Последний момент существенно отражается на эффективности работы алгоритма. Если нет оснований искусственно задать это условие, вообще говоря, рекомендуется использовать иерархические методы. Заметим также еще один момент, существенный для обеих групп алгоритмов: не всегда правильным решением является кластеризация всех наблюдений. Возможно, более аккуратным будет сначала очистить выборку от выбросов, а затем продолжить анализ. Можно также не задавать очень высоким критерий остановки.

Кластерный анализ - это статистический анализ, позволяющий получить разбиение большого объема данных на классы или группы (от англ, cluster - класс) согласно некоторому критерию или их совокупности.

Для проведения классификации данных Х х,...,Х п используют понятие метрики или расстояния.

Метрикой называется функция р отображающая некоторое метрическое пространство в пространство действительных чисел и обладающая следующими свойствами (аксиомами метрики):

• 1) р(ЗД>0,
• 2) p(X,Y)=p (Y,X),
• 3) р(Х, У) = 0 X = Y,
• 4) P (X,Y) P (Z,Y).

В теории кластерного анализа используются следующие метрики для измерения расстояния между отдельными точками (векторами):

1) евклидово расстояние

2) взвешенное евклидово расстояние

где w k - веса, пропорциональные важности признака в задаче классификации. Веса задают после проведения дополнительных исследований

и полагают, что ^ w* = 1;

• 3) хеммингово расстояние (или city-block) - расстояние по карте между кварталами в городе

4) расстояние Махаланобиса (или угол Махаланобиса)

где А - симметричная положительно определенная матрица весовых коэффициентов (часто выбирается диагональной); А - матрица ковариаций векторов Х 19 ...,Х п;

5) расстояние Минковского

Расстояния 1), 2), 3) или 5) используют в случае нормального распределения независимых случайных величин X l9 ...,X n ~N(M,A) или в случае их однородности по геохимическому смыслу, когда каждый вектор одинаково важен для классификации. Расстояние 4) используют в случае наличия ковариационной связи векторов Х х,...,Х п.

Выбор метрики осуществляется исследователем в зависимости от того, какой результат он хочет получить. Этот выбор неформализуем, так как зависит от многих факторов, в частности от ожидаемого результата, от опыта исследователя, уровня его математической подготовки и т. д.

В ряде алгоритмов наряду с расстояниями между векторами используются расстояниями между кластерами и объединениями кластеров.

Пусть S { - /-ый кластер, состоящий из n t векторов или точек. Пусть

X (l) - выборочное среднее по точкам, попадающим в кластер S f , или центр тяжести кластера 5.. Тогда различают следующие расстояния между кластерами, не имеющими внутри других кластеров:

1) расстояние между кластерами по принципу «ближнего соседа»

2) расстояние между кластерами по принципу «дальнего соседа»

3) расстояние между центрами тяжести групп

4) расстояние между кластерами по принципу «средней связи»

5) обобщенное расстояние по Колмогорову

Расстояние между кластерами, являющимися объединением других классов, можно вычислить по общей формуле:

где S^ k ^ - кластер, полученный объединением классов S k и S t .

Все частные случаи расстояний получаются из этой обобщенной формулы. При а = р = 1 / 2, 8 = -1/2, у = 0 имеем расстояние по принципу «ближнего соседа», при а = р = 5 = 1/ 2, у = О - «дальнего соседа»,

при а =---, р =--- ,5 = 0, у = 0 - расстояние по центрам тяже-

п к + n i п к + n i

сти групп.

Методы кластерного анализа подразделяются на I) агломеративные (объединяющие), II) дивизимные (разделяющие) и III) итеративные.

Первые последовательно объединяют отдельные объекты в кластеры, вторые, наоборот, расчленяют кластеры на объекты. Третьи объединяют первые два. Их особенностью является формирование кластеров, исходя из условий разбиения (так называемых параметров), которые могут быть изменены в процессе работы алгоритма для улучшения качества разбиения. Итеративные методы обычно используются для классификации больших объемов информации.

Рассмотрим подробнее агломеративные методы. Агломеративные методы являются наиболее простыми и распространенными среди алгоритмов кластерного анализа. На первом шаге каждый вектор или объект Х 19 ...,Х п исходных данных рассматривается как отдельный кластер или класс. По вычисленной матрице расстояний выбираются наиболее близкие друг к другу и объединяются. Очевидно, что процесс завершится через (п - 1) шаг, когда в результате все объекты будут объединены в один кластер.

Последовательность объединений можно представить в виде дендрограммы, или дерева. На рис. 1.18 показано, что на первом шаге были объединены векторы X t ,X 2 , так как расстояние между ними 0,3.

На втором шаге к ним был присоединен вектор Х 3 , отстоящий от кластера {Х 1 ,Х 2 } на расстояние 0,5, и т. д. На последнем шаге объединяются все векторы в один кластер.

Рис. 1.18.

К агломеративным относят методы одиночной, средней, полной связи и метод Уорда.

1. Метод одиночной связи. Пусть X v ...,X n - векторные данные, причем каждый вектор образует один кластер. Сначала вычисляется матрица расстояний между этими кластерами, причем в качестве метрики используется расстояние по принципу ближнего соседа. С помощью этой матрицы выбирают два наиболее близких вектора, которые и образуют первый кластер 5,. На следующем шаге между S ] и оставшимися векторами (которые мы считаем кластерами) вычисляется новая матрица расстояний, причем в качестве метрики используется расстояние между кластерами, объединенными в классы (а = р = 1/ 2, 5 = -1/2, у = 0). Ближайший к полученному ранее классу S { кластер объединяется с ним, образуя S 2 . И т. д. Через п- 1 шагов получаем, что все векторы объединены в один кластер.

Достоинства : 1) на каждом шаге алгоритма добавляется только один элемент, 2) метод чрезвычайно прост, 3) алгоритм нечувствителен к преобразованиям исходных данных (вращению, сдвигу, переносу, растяжению).

Недостатки : 1) необходимо постоянно пересчитывать матрицу расстояний, 2) число кластеров заранее известно и не может быть уменьшено

• 2. Метод полной связи. Метод практически повторяет метод одиночной связи за исключением того, что включение нового объекта в кластер происходит тогда и только тогда, когда расстояние между объектами (векторами или кластерами) меньше некоторого наперед заданного числа. Число задается пользователем. Расстояние вычисляется только по принципу «дальнего соседа» (то же самое можно сказать и про расстояние между классами, объединенными в классы - только принцип дальнего соседа при ос = р = 8 = 1/2, у = 0).
• 3. Метод средней связи. Алгоритм образования кластеров совпадает с алгоритмом одиночной связи, однако при решении вопроса о включении нового объекта в кластер вычисления производятся по принципу средней связи. Как и в методе полной связи, все вычисленные между кластерами расстояния сравниваются с задаваемым пользователем числом. И если оно (расстояние) меньше заданного числа, новый объект включается в старый класс. Таким образом, метод средней связи отличается от метода полной связи только способом вычисления расстояния между кластерами.
• 4. Метод УОРДА. Пусть Х 19 ...,Х п - данные, причем каждый вектор образует один кластер. Находим матрицу расстояний, используя какую-нибудь метрику (например, расстояние Махаланобиса), определяем по ней наиболее близкие друг к другу кластеры. Вычисляем сумму квадратов отклонений векторов внутри кластера S k по формуле:

где к - номер кластера, i - номер вектора в кластере, j - номер координаты X t е У1 Р, п к - число векторов в кластере, X jk - выборочное среднее X i в S k . Величина V k характеризует отклонения векторов друг от друга внутри кластера (нового S k +S f или старого^). Расчет V k следует проводить до и после объединения, причём нужно перебирать все возможные варианты таких объединений. В дальнейшем в кластер S k добавляются только те векторы или кластеры, которые приводят к наименьшему изменению V k после объединения и, как следствие, которые будут расположены на минимальном расстоянии от исходного кластера S k .

Рассмотрим далее итеративные методы. Сущность итеративных методов заключается в том, что кластеризация начинается с задания некоторых начальных условий. Например, требуется задать число получаемых кластеров или задать расстояние, определяющее конец процесса образования кластеров, и т. д. Начальные условия выбираются согласно результату, который нужен исследователю. Однако обычно они задаются по решению, найденному одним из агломеративных методов. К итеративным методам относят метод ^-средних и метод поиска сгущений.

1. Метод /г-средних. Пусть имеются векторы X l9 ...,X n e9F и их необходимо разбить на к кластеров. На нулевом шаге из п векторов случайным образом выбираем к из них, считая, что каждый образует один кластер. Получаем множество кластеров-эталонов,...,е[ 0) с весами

coj 0) ,...,X. и вычисляем матрицу расстояний между X. и эталонами е 1 (0) ,...,^ 0) по некоторой метрике, например по евклидовой:

На основе знания вычисленной матрицы расстояний вектор Х { помещается в тот эталон, расстояние до которого минимально. Допустим для определенности, что это. Он заменяется новым, пересчитанным с учетом присоединенной точки, по формуле

Кроме того, пересчитывается и вес:

Если в матрице встречается два или более минимальных расстояния, то X t включают в кластер с наименьшим порядковым номером.

На следующем шаге выбирают следующий вектор из оставшихся, и процедура повторяется. Таким образом, через (п-к ) шагов каждому

эталону е^~ к) будет соответствовать вес и процедура кластеризации завершится. При большом п и малом к алгоритм быстро сходится к устойчивому решению, т. е. к решению, в котором эталоны, полученные после первого применения алгоритма, совпадают по количеству и составу с эталонами, найденными при повторном применении метода. Тем не менее, алгоритмическую процедуру всегда повторяют несколько раз, используя полученное в предыдущих расчетах разбиение в качестве векторов-эталонов (как начальное приближение): найденные ранее эталоны е[ п к е (2 п к)к) принимаются за е (х 0) 9 ... 9 е (к 0) 9 и алгоритмическая процедура повторяется.

• 2. Метод поиска сгущений. Это следующий итеративный алгоритм. Он не требует априорного задания числа кластеров. На первом шаге вычисляется матрица расстояний между Х Х9 ... 9 Х п еУ1 р по какой-нибудь метрике. Затем случайным образом выбирают один вектор, который будет играть роль центра первого кластера. Это начальное приближение. Положим, что этот вектор лежит в центре р-мерной сферы радиуса R, причем этот радиус задается исследователем. После этого определяются векторы X Si ,... 9 X Sk , попавшие внутрь этой сферы, и по ним высчитывается выбо-
• - 1 к

рочное математическое ожидание X = ~У]Х 5 . Затем центр сферы пере-

носится в X , и расчетная процедура повторяется. Условием окончания итерационного процесса является равенство векторов средних X , найденных на т и (т+ 1) шагах. Попавшие внутрь сферы элементы Х 9 ... 9 Х

включаем в один кластер и исключаем их из дальнейшего исследования. Для оставшихся точек алгоритм повторяется. Алгоритм сходится при любом выборе начального приближения и любом объеме исходных данных. Однако для получения устойчивого разбиения (т. е. разбиения, в котором кластеры, найденные после первого применения алгоритма, совпадают по количеству и составу с кластерами, найденными при повторном применении метода) рекомендуется повторить алгоритмическую процедуру несколько раз при различных значениях радиуса сферы R. Признаком устойчивого разбиения будет образование одного и того же числа кластеров с одним и тем же составом.

Заметим, что задача кластеризации не имеет единственного решения. Как следствие, перебрать все допустимые разбиения данных на классы достаточно сложно и не всегда представляется возможным. Для того чтобы оценить качество различных способов кластеризации вводят понятие функционала качества разбиения, который принимает минимальное значение на наилучшем (с точки зрения исследователя) разбиении.

Пусть Х Х9 ... 9 Х п еУ1 Р - некоторая совокупность наблюдений, которая разбивается на классы S = {S l9 ... 9 S k } 9 причем к заранее известно. Тогда основные функционалы качества разбиения при известном числе кластеров имеют вид:

1) Взвешенная сумма внутриклассовых дисперсий

где а{1) - выборочное математическое ожидание кластера S l .

Функционал Q { (S) позволяет оценить меру однородности всех кластеров в целом.

2) Сумма попарных внутриклассовых расстояний между элементами или

где п 1 - число элементов в кластере S { .

3) Обобщенная внутриклассовая дисперсия

где n j - число элементов в S ., А; . - выборочная ковариационная матрица для Sj.

Функционал является средней арифметической характеристикой обобщенных внутриклассовых дисперсий, подсчитанных для каждого кластера. Как известно, обобщенная дисперсия позволяет оценить степень рассеивания многомерных наблюдений. Поэтому Q 3 (S) позволяет оценить средний разброс векторов наблюдений в классах S l9 ... 9 S k . Отсюда и его название - обобщенная внутриклассовая дисперсия. Q 3 (S) применяется в случае, когда необходимо решить задачу о сжатии данных или о сосредоточении наблюдений в пространстве с размерностью меньше исходной.

4) Качество классификации наблюдений можно оценить и с помощью критерия Хотеллинга. Для этого применим критерий для проверки гипотезы Н 0 о равенстве векторов средних двух многомерных совокупностей и вычислим статистику

где n t и п т - число векторов в классах S l ,S m ; X,Х т - центрированные исходные данные; S* - объединенная ковариационная матрица кластеров S n S m: S* =---(XjX l +X^X m) . Как и ранее, значение Q 4 (S )

п,+п т -2

сравнивают с табличным значением, вычисленным согласно формуле

где m - исходная размерность векторов наблюдений, а - уровень значимости.

Гипотеза Н 0 принимается с вероятностью (1-ос), если Q 4 (S) n _ m , и отвергается в противном случае.

Оценить качество разбиения на классы можно и эмпирически. Например, можно сравнивать выборочные средние, найденные для каждого класса, с выборочным средним всей совокупности наблюдений. Если они разнятся в два раза и более, то разбиение хорошее. Более корректное сравнение кластерных выборочных средних с выборочным средним всей совокупности наблюдений приводит к использованию дисперсионного анализа для оценки качество разбиения на классы.

Если число кластеров в S = {S l9 ...,S k } заранее неизвестно, то используют следующие функционалы качества разбиения при произвольно выбираемом целом m :

I I к 1 1 m

- - средняя мера внутриклас-

П i =1 n i XjeSj X"tSj J

сового рассеяния,

• (1 П / 1 W
• - X ~-~ r “ мера концентрации точек множества

п nV л J J

S, - число элементов в кластере, содержащем точку Х г

Заметим, что при произвольном значении параметра т функционал Z m (S) достигает минимума, равного I/ п, если исходное разбиение на кластеры S = {S l9 ...,S k } является разбиением на моно кластеры S. = {Xj }, так как V(X t) = 1. В то же время Z m (S ) достигает максимума, равного 1, если S - один кластер, содержащий все исходные данные,

так как V(X {) = n. В частных случаях можно показать, что Z_ l (S) = -, где к - число различных кластеров в S = {S l9 ... 9 S k } 9 Z X (S) = max - ,

*" V п)

где n t - число элементов в кластере S i9 Z^(S) = min - ,

г " п)

Заметим, что в случае неизвестного числа кластеров функционалы качества разбиения Q(S) можно выбирать в виде алгебраической комбинации (суммы, разности, произведения, отношения) двух функционалов I m (S), Z m (S), так как первый является убывающей, а другой - возрастающей функцией числа классов к. Такое поведение Z m (S)

гарантирует существование экстремума Q(S ).

При большом количестве наблюдений иерархические методы кластерного анализа не пригодны. В таких случаях используют неиерархические методы, основанные на разделении, которые представляют собой итеративные методы дробления исходной совокупности. В процессе деления новые кластеры формируются до тех пор, пока не будет выполнено правило остановки .

Такая неиерархическая кластеризация состоит в разделении набора данных на определенное количество отдельных кластеров. Существует два подхода. Первый заключается в определении границ кластеров как наиболее плотных участков в многомерном пространстве исходных данных, т.е. определение кластера там, где имеется большое "сгущение точек". Второй подход заключается в минимизации меры различия объектов

Алгоритм k-средних (k-means)

Наиболее распространен среди неиерархических методов алгоритм k-средних , также называемый быстрым кластерным анализом . Полное описание алгоритма можно найти в работе Хартигана и Вонга (Hartigan and Wong, 1978). В отличие от иерархических методов, которые не требуют предварительных предположений относительно числа кластеров, для возможности использования этого метода необходимо иметь гипотезу о наиболее вероятном количестве кластеров.

Алгоритм k-средних строит k кластеров, расположенных на возможно больших расстояниях друг от друга. Основной тип задач, которые решает алгоритм k-средних , - наличие предположений (гипотез) относительно числа кластеров, при этом они должны быть различны настолько, насколько это возможно. Выбор числа k может базироваться на результатах предшествующих исследований, теоретических соображениях или интуиции.

Общая идея алгоритма: заданное фиксированное число k кластеров наблюдения сопоставляются кластерам так, что средние в кластере (для всех переменных) максимально возможно отличаются друг от друга.

Описание алгоритма

1. Первоначальное распределение объектов по кластерам.

   Выбирается число k, и на первом шаге эти точки считаются "центрами" кластеров. Каждому кластеру соответствует один центр.

   Выбор начальных центроидов может осуществляться следующим образом:

   • выбор k-наблюдений для максимизации начального расстояния;
   • случайный выбор k-наблюдений;
   • выбор первых k-наблюдений.

   В результате каждый объект назначен определенному кластеру.

2. Итеративный процесс.

   Вычисляются центры кластеров , которыми затем и далее считаются покоординатные средние кластеров. Объекты опять перераспределяются.

   Процесс вычисления центров и перераспределения объектов продолжается до тех пор, пока не выполнено одно из условий:

   • кластерные центры стабилизировались, т.е. все наблюдения принадлежат кластеру, которому принадлежали до текущей итерации;
   • число итераций равно максимальному числу итераций.

   На рис. 14.1 приведен пример работы алгоритма k-средних для k, равного двум.

Рис. 14.1.

Выбор числа кластеров является сложным вопросом. Если нет предположений относительно этого числа, рекомендуют создать 2 кластера, затем 3, 4, 5 и т.д., сравнивая полученные результаты.

алгоритм может медленно работать на больших базах данных. Возможным решением данной проблемы является использование выборки данных.