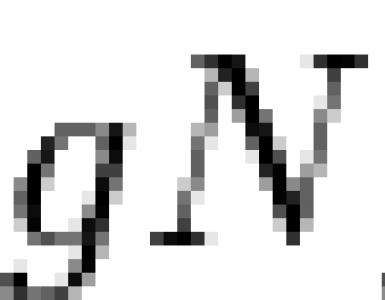Нормальний дільник групи. Нормальні дільники груп

Суміжні класи. Розкладання групи за підгрупою

Нехай група, її підгрупа, довільний елемент групи . Складемо безліч. Це непорожня множина, називається лівим суміжним класомгрупи за підгрупою, що визначається елементом. Безліч називається правим суміжним класомгрупи за підгрупою, що визначається елементом. У загальному випадку .

Завдання 61.У знайти правий і лівий суміжні класи, що визначаються елементом, якщо підгрупа.

Рішення.

Складемо класи

Зауважимо, .

Нехай – група та – її підгрупа.

Якщо , то кажуть, що група підгрупою розкладена на один суміжний клас.

Якщо, то існує елемент і тоді складемо клас.

Якщо , то кажуть, що група по підгрупі розкладена на два ліві суміжні класи .

Якщо, то маємо розкладання групи на три суміжні класи за підгрупою і т.д.

Процес розкладання групи за підгрупою на ліві суміжні класи може бути кінцевим, може бути нескінченним.

Аналогічно можна отримати розкладання групи по підгрупі на праві суміжні класи: .

Праве розкладання має співпадати з лівим розкладанням.

В результаті ми отримуємо дві множини класів:

І - ліве і праве фактор-множини множини за підмножиною. Довжина цих множин називається індексомпідгрупи у групі.

Завдання 62.Знайти фактор-множину множини по підгрупі щодо операції додавання.

Рішення.Операція додавання в комутативна, тому ліве і праве розкладання будуть однакові. Розкладемо на ліві суміжні класи.

Наприклад, . Будуємо. . Маємо розкладання на два суміжні класи. Чинник-множина: .

Завдання 63.У мультиплікативній групі

Візьмемо підгрупу. Знайти фактор-множина множини по .

Рішення.При лівому розкладі маємо:

Т. е. Лівосторонній фактор-множина.

При правосторонньому розкладанні маємо:

Т. е. Правостороннє фак-тор-множина, причому,.

Індекс підгрупи дорівнює 3.

Завдання 64.Знайти розкладання адитивної групи по підгрупі цілих чисел, кратних 3.

Рішення. .

Наприклад, . Складемо. Отже, клас складається з усіх цілих чисел, які при розподілі на 3 дають у залишку 1. , наприклад, , . Складемо. Отже, клас складається з усіх цілих чисел, які при розподілі на 3 дають у залишку 2. Отже, знаходяться всі цілі числа, які при розподілі на 3 дають у залишку 0, в класі – всі цілі числа, які діляться на 3 дають в залишку 1, у класі – всі числа із залишком 2. Але за розподілі на 3 можливі лише залишки 0, 1, 2. Отже, всі цілі числа розподілилися за класами , т. е. розкладання на суміжні класи має вигляд: . Оскільки додавання в комутативне, то лівостороннє розкладання збігається з правостороннім. Індекс підгрупи дорівнює 3.

Нормальний дільник групи. Фактор-група

Якщо групі щодо підгрупи за будь - якого елементі , т. е. якщо будь - який елемент групи перестановлений з підгрупою , то підгрупа називається нормальним дільником групи .

Якщо операція групи коммутативна, то будь-яка підгрупа групи є нормальним дільником. Якщо при лівому і правосторонньому розкладанні групи по підгрупі суміжні класи, куди розпадається група , виходять однаковими, то – нормальний дільник групи . Правильне і зворотне: якщо – нормальний дільник групи , то за лівому і правосторонньому розкладанні групи по підгрупі суміжні класи, куди розпадається група , виходять однаковими.

Є нормальним дільником групи тоді і лише тоді, коли за будь-якого і будь-якого елемента .

Завдання 65.Якщо індекс підгрупи групи дорівнює 2, то нормальний дільник групи .

Рішення.Якщо підгрупа має індекс 2 у групі, то де і, тобто. Отже, класи суміжності лівостороннього розкладання збігаються з відповідними класами правостороннього розкладання, тобто нормальний дільник групи .

Завдання 66.Чи буде група у завданні 63 нормальним дільником у групі?

Рішення.Лівостороннє розкладання групи по підгрупі складається з класів, і. Правостороннє розкладання складається з класів , , , але , , т. е. підгрупа перестав бути нормальним дільником групи .

Завдання 67.Знайти фактор-групу групи за підгрупою всіх чисел, кратних 3.

Рішення.Оскільки додавання комутативно, то – нормальний дільник. Знайдемо розкладання по: . Фактор-множина складається з класів. Задамо на операцію додавання:

Заповнення таблиці Келі здійснюється за правилом:

Наприклад, . Це безліч складається з усіх цілих чисел, де, тобто. Тоді. Отже, ми отримали фактор-групу, операція додавання в якій задана вищевказаною таблицею Келі.

Завдання 68.Знайти фактор-групу групи за підгрупою.

Рішення.- Нормальний дільник, т. К. Додавання в комутативно. Знайдемо розкладання по: . Дійсно, зобразимо на числовій осі, а елементи відзначимо на ній крапками:

Побудуємо, де. Якщо , то якщо , то елементи відзначимо зірочками. Тоді складається з елементів, відмічених точками та зірочками. У цю множину не потрапляє елемент, наприклад, . Тоді будуємо безліч, елементи якого позначимо штрихом. Тоді складається з елементів, позначених точками, зірочками та штрихами, але не збігається з . Очевидно, щоб збіглося з , необхідно, щоб .

Ми побудували фактор-множину. Відповідно до процедури факторизації, операція додавання визначається так: , де , .

Вступ 2
1. Визначення та приклади груп 4
2. Підгрупи 8
3. Циклічні групи. 13
4. Нормальні дільники, фактор-групи 17
5. Ідеал підгрупи у групі. Теорема Лагранжа та наслідки з неї. 22
6. Використання нормальних дільників груп під час вирішення завдань 26
Висновок 29
Список літератури 30

Вступ

Вища алгебра є далеко що йде, але цілком природне узагальнення основного змісту шкільного курсу елементарної алгебри. Лінійна алгебра, що є великою наукою, присвяченої в основному теорії матриць і пов'язаної з нею теорії лінійних перетворень векторних просторів, включає також теорію форм, теорію інваріантів і тензорну алгебру, що відіграє важливу роль у диференціальній геометрії. Теорія векторних просторів отримує розвиток поза алгебри, у функціональному аналізі (нескінченномірні простору). За різноманітністю і значущістю додатків як у математиці, так і в механіці, фізиці та технічних науках лінійна алгебра залишається поки що першою серед численних гілок алгебри.
Теорія полів виявилася природною областю для подальшого розвитку теорії рівнянь, а її основні гілки – теорія полів алгебраїчних чисел та теорія полів алгебраїчних функцій – пов'язали її, відповідно, з теорією чисел та теорією функцій комплексного змінного. Курс вищої алгебри включає елементарне введення в теорію полів, а деякі розділи курсу - багаточлени від декількох невідомих, нормальна форма матриці - викладаються відразу для випадку довільного основного поля.
Більше широким, ніж поняття поля, є поняття кільця. На відміну від випадку поля, тут вже не потрібна здійсненність поділу і, крім того, множення може бути некомутативним і навіть неасоціативним. Найпростішими прикладами кілець є сукупність всіх цілих чисел (включаючи і негативні), система многочленів від одного невідомого і система дійсних функцій дійсного змінного. Теорія кілець включає такі старі гілки алгебри, як теорія гіперкомплексних систем і теорія ідеалів, вона пов'язана з низкою математичних наук/зокрема з функціональним аналізом, і вже знайшла деякі виходи у фізику. Курс вищої алгебри, сутнісно, ​​містить лише визначення поняття кільця.
Ще більшу область застосувань має теорія груп. Групою називається алгебраїчна система з однією основною операцією, причому ця операція повинна бути асоціативною, хоча необов'язково комутативною, і повинна мати зворотну операцію - поділ, якщо основна операція названа множенням. Така, наприклад, сукупність цілих чисел, що розглядається щодо операції додавання, а також сукупність позитивних дійсних чисел, що розглядається з операцією множення. Групи грали велику роль вже в теорії Галуа, у питанні про розв'язання рівнянь у радикалах, зараз вони є важливим знаряддям у теорії полів, у багатьох розділах геометрії, у топології, а також поза математикою - в кристалографії, в теоретичній фізиці. Взагалі, за широтою області додатків теорія груп займає серед усіх гілок алгебри наступне після лінійної алгебри місце.
Предметом даної є нормальні дільники груп.
Завдання:
1. Дати визначення групі та підгрупі, розглянути приклади груп.
2. Розглянути циклічні групи.
3. Розглянути поняття нормальних дільників
4. Навести теорему Лагранжа та наслідки з неї.
5. Розглянути використання нормальних дільників груп під час вирішення завдань.

Список використаних джерел

1. Куликов Л.Я. і теорія чисел: Навч. посібник для педагогічних інститутів. – : Вищ. школа, 1979. - 559 с., Іл.
2. Кострикін А.І. Введення в алгебру: Підручник для вузів. - М.: Фізматліт, 2004. - 272 с.
3. Фаддєєв Д.К. Збірник завдань із вищої алгебри. - М.: Наука, 1977. - 288 с.
4. Курош А.Г. Курс найвищої алгебри. - М.: Наука, 1968.
5. Окунєв Л.Я. Збірник завдань із вищої алгебри – М.: Просвітництво, 1964.

Загальний об'єм: 30 стор.

Рік: 2013

Визначення

Підгрупа Nгрупи Gназивається нормальноюякщо вона інваріантна щодо сполучень, тобто для будь-якого елемента nз Nта будь-якого gз G, елемент gng − 1 лежить у N :

Наступні умови нормальності підгрупи еквівалентні:

Умова (1) логічно слабша, ніж (2), а умова (3) логічно слабша, ніж (4). Тому умови (1) та (3) часто використовуються при доказі нормальності підгрупи, а умови (2) та (4) використовуються для доказу наслідків нормальності.

Приклади

• {e) та G- завжди нормальні підгрупи G. Вони називаються тривіальними. Якщо інших нормальних підгруп немає, то група Gназивається простий.

• Центр групи – нормальна підгрупа.

• Комутант групи – нормальна підгрупа.

• Будь-яка характеристична підгрупа нормальна, оскільки поєднання - це автоморфізм.

• Усі підгрупи Nабелевої групи Gнормальні, оскільки gN = Ng . Неабелева група, яка має будь-яка підгрупа нормальна, називається гамільтонової.

• Група паралельних переносів у просторі будь-якої розмірності - нормальна підгрупа евклідової групи; наприклад, у тривимірному просторі поворот, зсув і поворот у зворотний бік призводить до простого зсуву.

• У групі кубика Рубика, підгрупа, що складається з операцій, що діють тільки на кутові елементи, нормальна, тому що ніяке сполучене перетворення не змусить таку операцію діяти на крайовий, а не кутовий елемент. Навпаки, підгрупа, що складається лише з поворотів верхньої грані, не нормальна, оскільки сполучення дозволяють перемістити частини верхньої грані вниз.

Властивості

• Нормальність зберігається при сюр'єктивних гомоморфізмах та взяття зворотних образів.
• Нормальність зберігається при побудові прямого твору.
• Нормальна підгрупа нормальної підгрупи має бути нормальної групи, тобто нормальність не транзитивна . Проте характеристична підгрупа нормальної підгрупи є нормальною.
• Кожна підгрупа індексу 2 нормальна. Якщо p- найменший простий дільник порядку G, то будь-яка підгрупа індексу pнормальна.
• Якщо N- нормальна підгрупа в G, то на безлічі лівих (правих) суміжних класів G / Nможна запровадити групову структуру за правилом

(g 1 N)(g 2 N) = (g 1 g 2)N Отримана множина називається факторгрупою Gпо N .

• Nнормальна тоді і лише тоді, коли вона тривіально діє на лівих суміжних класах G / N .

Історичні факти

Еваріст Галуа першим зрозумів важливість нормальних підгруп.

Посилання

• Вінберг Е. Б.Курс алгебри – М.: Видавництво «Факторіал Прес», 2002, ISBN 5-88688-060-7

Wikimedia Foundation. 2010 .

• Нормальний алгоритм Маркова
• Нормальний електродний потенціал

Дивитись що таке "Нормальний дільник" в інших словниках:

Нормальний дільник- інваріантна підгрупа, одне з основних понять теорії груп, введене Е. Галуа. Н. д. групи G підгрупа Н, для якої gH = Hg за будь-якого вибору елемента g групи G … Велика Радянська Енциклопедія

НОРМАЛЬНИЙ ДІЛЬНИК- нормальна підгрупа, інваріантна підгрупа, підгрупа Нгрупи G, для якої лівостороннє розкладання групи Gпо підгрупі Нзбігається з правостороннім, тобто така підгрупа, що для будь-якого елемента суміжні класи аН і На рівні (у сенсі… … Математична енциклопедія

Нормальний ряд підгруп- Для загального опису теорії груп див. Група (математика) та Теорія груп. Курсив означає посилання на цей словник. # А Б В Г Д Е Ї З Д І Й К Л М Н О П Р С Т У … Вікіпедія

Нормальний ряд- Для загального опису теорії груп див. Група (математика) та Теорія груп. Курсив означає посилання на цей словник. # А Б В Г Д Е Й З І Й К Л М Н О П Р С Т У … Вікіпедія – топологічна група, компактна як топологічна. простір. Напр., всяка кінцева група (у дискретній топології) є К. г. Алгебраїчна група, хоча вона і є компактним топологічним. простором (щодо топології Заріського)... Математична енциклопедія

ЧИ - КОВЧИНА ТЕОРЕМА- Розв'язувана підгрупа Gгрупи GL(V)(V кінцевомірний векторний простір над замком алгебри) має нормальний дільник G1 індексу не більше де р залежить тільки від dim V, такий, що в Vіснує прапор інваріантний щодо G1. Математична енциклопедія

ТОПОЛОГІЧНА ГРУПА- безліч G, на кром задані дві структури групи і топологіч. простори, узгоджені умовою безперервності групових операцій. А саме, відображення прямого твору G має бути безперервним. Підгрупа Н Т. р. G є Т. р. в ... Математична енциклопедія

Теорема Лагранжа стверджує, що якщо , a
, то

тобто. порядок
будь-якої підгрупи H групи G ділить N – порядок групи G.

Природно, виникає питання про теорему: якщо m є дільником
, то чи існує групі G підгрупа H порядку m?

Іншими словами: чи існує для кожного дільника m порядку групи N підгрупи H групи G порядку m?

У загальному випадку відповідь негативна, проте в деяких окремих випадках така зверненнятеореми Лагранжа справедливо.

Теорема. (звернення теореми Лагранжа )

1. Будь-яка підгрупа циклічної групи знову є циклічна група.

2. Підгрупи нескінченної циклічної групи

.

3. Підгрупи циклічної групи порядку числа .

Доведення.

Доведемо 1 . Нехай - Довільна циклічна група порядку
. Для певності будемо припускати, що - Адитивна група.

І тут загальний елемент групи має вигляд

Нехай
- Довільна непоодинока підгрупа групи , тобто.
.

Так як
, то елементами підгрупи
є елементи виду
, але якщо.

Серед усіх елементів виду
, виберемо елемент

, де
- Найменше позитивне число.

Тоді будь-яке
можна уявити у вигляді:

З того, що

але m – найменше число, що задовольняє умову

mgH  r = 0  H = ,

тобто. Н - циклічна група з утворюючим елементом mg.

Доведемо 2 . Підгрупи нескінченної циклічної групи
вичерпуються нескінченними групами
.

Справді, оскільки
- циклічна група з утворюючим елементом 1 або
, тобто.

то, відповідно до пункту 1 даної теореми, будь-яка підгрупа H циклічної групи
визначається натуральним числом
і має вигляд

причому всі ці підгрупи нескінченні.

Доведемо 3 . Підгрупи циклічної групи порядку знаходяться у взаємно однозначній відповідності до позитивних дільників числа .

Нехай, як і раніше,
- Адитивна циклічна група порядку , тобто.

Якщо , причому, якщо елемент

Нам треба довести, що
ділить .

Справді, уявимо

Тоді з того, що

,

а мінімальність
тягне
, отже
.

Таким чином, з того, що
слід, що підгрупа
має порядок , тобто.

.

Коли
пробігає по всіх позитивних дільниках числа , те саме робить і , і ми отримуємо рівно по одній підгрупі порядку , що ділить .

Слідство. У циклічній групі
порядку підгрупа
порядку
збігається з безліччю елементів
, таких, що
.

Доведення. Елементи циклічної групи
порядку мають вигляд

Якщо
, Тої
.

Назад, нехай
і
.

З умови
випливає, що
, звідки
в.

1. Нормальні дільники

Нехай G – довільна група, а H – підгрупа групи G, тоді, якщо ми отримуємо два ліві суміжні класи
і
.

Ми хочемо з'ясувати умови, за яких добуток елементів, взятих із суміжних класів
і
, залежить від вибору представників класів і належить одному й тому суміжному класу, як і добуток елементів
, а саме класу
.

Елемент належить суміжному класу
, а елемент - суміжному класу
.

Довільні елементи, що належать відповідно до суміжних класів
і
можна уявити у вигляді:

Тоді їхній твір

має належати класу

.

Це означає, що у підгрупі H,

Помножуючи почленно отриману рівність зліва на , маємо:

(9)

де

Співвідношення (9) дозволяє зробити наступний висновок.

Оскільки елементи
вибрані довільно, то для будь-якого елемента
та будь-якого елемента
існує елемент

,

що задовольняє співвідношенню (9).

Крім того, елемент
а елемент
. Внаслідок цього кожен лівий суміжний клас групи G по H міститься в деякому правому суміжному класі групи G по тій же підгрупі H:

Аналогічно можна показати і зворотне включення

а це означатиме, що

Визначення 1. Підгрупа H групи G називається нормальним дільникомабо інваріантною підгрупоюякщо для будь-яких двох суміжних класів g 1 H і g 2 H за підгрупою H, твір
довільних елементів
з цих класів належить одному й тому ж суміжному класу
(Рис. 2).

Мал. 2– Підгрупа H – звичайний дільник групи G.

Формально: підгрупа H - нормальний дільникгрупи , якщо:

У комутативних групах будь-яка підгрупа є звичайним дільником (через комутативності операції складання).

Для практичного використання поняття нормального дільника розглянемо ще кілька «конструктивніших у зверненні» визначень.

Визначення 2. Підгрупа H групи G є нормальним дільникомгрупи G у тому й лише тому випадку, якщо кожен лівий суміжний клас
збігається з правим суміжним класом
групи G по H і навпаки.

Формально: підгрупа H - нормальний дільникгрупи G, якщо:

Умова (12), очевидно, означає, що:

приклади.

1. У будь-якій групі G сама група
та одинична підгрупа
є її нормальними дільниками: лівий та правий суміжні класи групи G за підгрупою
складається з одного суміжного класу
а лівий (правий) суміжні класи по одиничній підгрупі H складаються з усіх елементів групи G.

2. У кожній групі G G кожна її підгрупа H є нормальним дільником.

3. Мультиплікативна група позитивних дійсних чисел
є нормальним дільником мультиплікативної групи всіх відмінних від нуля дійсних чисел,

4. Мультиплікативна група, відмінних від нуля раціональних чисел
є нормальним дільником мультиплікативної групи відмінних від нуля дійсних чисел

5. У мультиплікативній групі
невироджених матриць
-го порядку з речовими коефіцієнтами підгрупа
матриць з визначником рівним одиниці:

є звичайним дільником цієї групи.

Справді, одинична матриця
, якщо

і

– відповідно, лівий та правий суміжні класи групи
-невироджених матриць
-го порядку з речовими коефіцієнтами за підгрупою
- матриць із визначником рівним одиниці.

,

Тобто.
.

З іншого боку, якщо

,

оскільки
тому

Отже, згрупувавши в один суміжний клас (лівий або правий) усі матриці з рівними детермінантами, отримаємо розкладання групи
по підгрупі
. Цей приклад показує, що у некомутативних групах може бути підгрупи – нормальні дільники, котрим лівий суміжний клас

збігається з правим суміжним класом

Підгрупа Hгрупи Gназивається нормальним дільником, якщо для кожного елемента gгрупи Gйого лівий та правий суміжні класи за підгрупою Hрівні, тобто. gH=Hg.

Теорема 2.5. Підгрупа Hгрупи Gє нормальним дільником тоді і тільки тоді, коли міститься в Hза будь-яких gз Gі hз H.

Доведенняочевидно.

Нехай H- Нормальний дільник групи G. На множині суміжних класів введемо операцію множення, що індукується груповою операцією. Під твором суміжних класів aHі bHбудемо розуміти безліч різноманітних творів елементів з aHна елементи bH. Оскільки H– нормальний дільник, всі ці твори містяться у суміжному класі ( ab)H. Таким чином, на багатьох суміжних класах введено операцію. Ця операція асоціативна ( aHbH)cH=aH(bHcH), існує нейтральний елемент H, і для кожного елемента aHіснує зворотний a -1 H. Отже, безліч суміжних класів щодо введеної операції утворюють групу, яка називається факторгрупою.

Гомоморфізм груп.

Однозначне відображення групи Gу групу H, що зберігає операцію, називається гомоморфізм групи Gв H.

Ізоморфізм є окремим випадком гомоморфізму.

Властивість 2.9. При гомоморфізм нейтральний елемент групи Gвідображається в нейтральний елемент групи H.

Доведеннявипливає з рівності.

Безліч елементів групи G, Що відображаються в нейтральний елемент, називають ядром гомоморфізму та позначають .

Властивість 2.10.

Доведення. Так як, то.

Властивість 2.11. Ядро гомоморфізму є нормальним дільником групи G.

Доведення. Для aз Gі bз ядра справедливо, тобто.

Безліч елементів групи H, що є образами елементів Gназивають безліччю образів і позначають .

Властивість 2.12. Безліч образів є підгрупою H.

Доведенняочевидно.

Теорема 2.6. Факторгрупа ізоморфна.

Доведення. Відповідність є взаємно однозначною і зберігає операцію, отже вона визначає ізоморфізм і .

Теорема 2.7. Для будь-якого нормального дільника Hгрупи Gіснує гомоморфізм, ядро ​​якого дорівнює H. Зокрема таким гомоморфізмом з Gв G/Hє.

Доведенняочевидно.

Нормальний ряд

Доведемо дві теореми про гомоморфізми.

Теорема 2.8. Нехай Hнормальний дільник групи Gі P- Підгрупа G. Тоді – нормальний дільник Pі

Доведення. Нехай і. Тоді так як Hнормальний дільник G, і тому всі елементи з P. Отже, - нормальний дільник P. Відповідність є взаємно однозначною і зберігає операцію. Теорему доведено.

Теорема 2.9. Нехай P– нормальний дільник та . Тоді T– нормальний дільник Gі .

Доведення. Розглянемо, де,. Оскільки , то , і значить T– нормальний дільник G. Відповідність взаємно однозначним, т.к. та зберігає операцію.

Група називається простою, якщо в ній немає нормального дільника відмінного від неї самої та одиничної підгрупи.

Нормальний ряд групи – послідовність підгруп, у якій кожна наступна нормальний дільник попередньої. Якщо всі групи нормального ряду містяться в нормальному ряді, то говорять, що другий нормальний ряд отриманий ущільненням першого нормального ряду.

Нормальний ряд без повторень, який не можна ущільнити, називається композиційним.

Для нормального ряду визначено фактори . Два нормальні ряди називаються ізоморфними, якщо всі фактори першого ряду ізоморфні факторам другого ряду переставленим у визначеному порядку.

Властивість 2.13. Якщо нормальні ряди та ізоморфні, то для кожного ущільнення першого ряду можна знайти ізоморфне ущільнення йому другого ряду.

Доведення.Допустимо, що між підгрупами і з'явилися нові підгрупи. Оскільки і, отже, фактори ізоморфні відповідним підгруп. Позначимо через відповідну підгрупу. Визначимо послідовність груп , де i=1,…,t. По доведеній вище теоремі. Таким чином, ущільнення другого ряду груп є ізоморфним. властивість доведено.