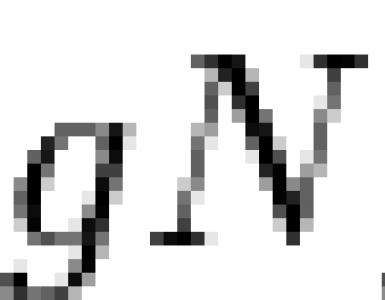ნორმალური ჯგუფის გამყოფი. ნორმალური ჯგუფის გამყოფები ნორმალური ჯგუფის გამყოფი

დაკავშირებული კლასები. ჯგუფის დაშლა ქვეჯგუფად

მოდით იყოს ჯგუფი, იყოს მისი ქვეჯგუფი და იყოს ჯგუფის თვითნებური ელემენტი. მოდით გავაკეთოთ ნაკრები. ეს არა ცარიელი ნაკრები ე.წ მარცხენა კოსეტიჯგუფები ელემენტის მიერ განსაზღვრული ქვეჯგუფების მიხედვით. კომპლექტი ე.წ სწორი კოსეტიჯგუფები ელემენტის მიერ განსაზღვრული ქვეჯგუფების მიხედვით. Ზოგადად .

პრობლემა 61. B იპოვეთ ქვეჯგუფის ელემენტის მიერ განსაზღვრული მარჯვენა და მარცხენა კოსეტები.

გამოსავალი.

შევქმნათ კლასები

Შენიშვნა, .

იყოს ჯგუფი და იყოს მისი ქვეჯგუფი.

თუ , მაშინ ამბობენ, რომ ჯგუფი ქვეჯგუფის მიხედვით დაიშალა ერთ კოსეტად.

თუ, მაშინ არის ელემენტი და ჩვენ შევქმნით კლასს.

თუ , მაშინ ნათქვამია, რომ ჯგუფი დაიშალა ქვეჯგუფის მიერ ორ მარცხენა კოსეტად.

თუ , მაშინ გვაქვს ჯგუფის დაშლა სამ კოსეტად ქვეჯგუფის მიმართ და ა.შ.

ჯგუფის ქვეჯგუფად მარცხენა კოსეტებად დაშლის პროცესი შეიძლება იყოს სასრული ან უსასრულო.

ანალოგიურად, ჩვენ შეგვიძლია მივიღოთ ჯგუფის დაშლა ქვეჯგუფების მიხედვით სწორ კოსეტებად: .

მარჯვენა დაშლა არ უნდა ემთხვეოდეს მარცხენა დაშლას.

შედეგად, ჩვენ ვიღებთ კლასების ორ კომპლექტს:

და არის სიმრავლის მარცხენა და მარჯვენა ფაქტორების სიმრავლეები ქვესიმრავლების მიხედვით. ამ კომპლექტების სიგრძეს ე.წ ინდექსიქვეჯგუფები ჯგუფში.

პრობლემა 62.იპოვეთ სიმრავლის ფაქტორების სიმრავლე ქვეჯგუფების მიხედვით შეკრების მოქმედების მიმართ.

გამოსავალი.დამატების მოქმედება არის კომუტაციური, ამიტომ მარცხენა და მარჯვენა გაფართოებები ერთნაირი იქნება. მოდით დავშალოთ მარცხენა კოსეტებად.

Მაგალითად, . ჩვენ ვაშენებთ. . გვაქვს დაშლა ორ მიმდებარე კლასად. ფაქტორების ნაკრები: .

პრობლემა 63.გამრავლების ჯგუფში

ავიღოთ ქვეჯგუფი. იპოვეთ სიმრავლის ფაქტორების სიმრავლე .

გამოსავალი.მარცხენა გაფართოებით გვაქვს:

ანუ მარცხნივ ფაქტორების ნაკრები.

მარჯვენა გაფართოებით გვაქვს:

ეს არის მარჯვენა გვერდითი ფაქტორების ნაკრები და , .

ქვეჯგუფის ინდექსი არის 3.

პრობლემა 64.იპოვეთ დანამატის ჯგუფის დაშლა მთელი რიცხვების ქვეჯგუფში, რომლებიც არიან 3-ის ჯერადი.

გამოსავალი. .

Მაგალითად, . მოდი შევადგინოთ. მაშასადამე, კლასი შედგება ყველა მთელი რიცხვისგან, რომლებიც 3-ზე გაყოფისას ტოვებენ ნაშთს 1-ს, მაგალითად, , . მოდი შევადგინოთ. შესაბამისად, კლასი შედგება ყველა მთელი რიცხვისგან, რომლებიც 3-ზე გაყოფისას ტოვებენ ნაშთს 2-ს. ასე რომ, in არის ყველა ის რიცხვი, რომელიც 3-ზე გაყოფისას ტოვებს ნაშთს 0-ს, კლასში არის ყველა რიცხვი, რომელიც იყოფა. 3-ით, ნაშთში 1-ის მიცემა, კლასში - ყველა რიცხვი ნაშთით 2-ით. მაგრამ როდესაც იყოფა 3-ზე, შესაძლებელია მხოლოდ ნაშთები 0, 1, 2. ეს ნიშნავს, რომ ყველა მთელი რიცხვი ნაწილდება კლასებში, ანუ იშლება მიმდებარე კლასებად. მიერ აქვს ფორმა: . ვინაიდან დამატება არის კომუტაციური, მარცხენა გაფართოება ემთხვევა მარჯვენა გაფართოებას. ქვეჯგუფის ინდექსი არის 3.

ნორმალური ჯგუფის გამყოფი. ფაქტორების ჯგუფი

თუ ჯგუფს აქვს ფარდობითი ქვეჯგუფი რომელიმე ელემენტისთვის, ანუ თუ ჯგუფის რომელიმე ელემენტი გადადის ქვეჯგუფთან, მაშინ ქვეჯგუფს ეწოდება ჯგუფის ნორმალური გამყოფი.

თუ ჯგუფში ოპერაცია არის კომუტაციური, მაშინ ჯგუფში ნებისმიერი ქვეჯგუფი არის ნორმალური გამყოფი. თუ ჯგუფის ქვეჯგუფად მარცხნივ და მარჯვნივ დაშლით, კოსეტები, რომლებშიც ჯგუფი იშლება, იდენტურია, მაშინ ეს არის ჯგუფის ნორმალური გამყოფი. პირიქითაც მართალია: თუ ჯგუფში ნორმალური გამყოფია, მაშინ ჯგუფის ქვეჯგუფად მარცხნივ და მარჯვნივ დაშლით, კოსეტები, რომლებშიც ჯგუფი იშლება, იდენტურია.

არის ჯგუფის ნორმალური გამყოფი თუ და მხოლოდ თუ რომელიმე ელემენტისთვის.

პრობლემა 65.თუ ჯგუფის ქვეჯგუფის ინდექსი არის 2, მაშინ არის ჯგუფის ნორმალური გამყოფი.

გამოსავალი.თუ ქვეჯგუფს აქვს ჯგუფში 2 ინდექსი, მაშინ სად და, ე.ი. შესაბამისად, მარცხნივ დაშლის კოსეტები ემთხვევა მარჯვენა მხარის დაშლის შესაბამის კლასებს, ანუ არის ჯგუფის ნორმალური გამყოფი.

პრობლემა 66.იქნება თუ არა 63-ე ამოცანის ჯგუფი ჯგუფში ნორმალური გამყოფი?

გამოსავალი.ჯგუფის მარცხენა მხარეს დაშლა ქვეჯგუფად შედგება კლასებისგან და . მარჯვენა დაშლა შედგება კლასებისგან, , , მაგრამ , , ანუ ქვეჯგუფი არ არის ჯგუფის ნორმალური გამყოფი.

პრობლემა 67.იპოვეთ ჯგუფის ფაქტორების ჯგუფი, რომელიც მოცემულია ყველა რიცხვის ქვეჯგუფში, რომელიც არის 3-ის ჯერადი.

გამოსავალი.ვინაიდან დამატება არის კომუტაციური, ის ნორმალური გამყოფია. ვიპოვოთ გაფართოება: . ფაქტორების ნაკრები შედგება კლასებისგან. დავაყენოთ დამატების ოპერაცია:

კეილის ცხრილის შევსება ხორციელდება წესის მიხედვით:

Მაგალითად, . ეს ნაკრები შედგება ყველა მთელი რიცხვისგან, სადაც, ე.ი. მაშინ . ამრიგად, ჩვენ მივიღეთ ფაქტორების ჯგუფი, რომლის შეკრების ოპერაცია მოცემულია ზემოთ ხსენებული კეილის ცხრილით.

პრობლემა 68.იპოვეთ ჯგუფის ფაქტორების ჯგუფი ქვეჯგუფების მიხედვით.

გამოსავალი.არის ნორმალური გამყოფი, რადგან მიმატება არის კომუტაციური. ვიპოვოთ გაფართოება: . მართლაც, მოდით გამოვსახოთ იგი რიცხვით ღერძზე და აღვნიშნოთ მასზე არსებული ელემენტები წერტილებით:

სად ავაშენოთ. თუ , მაშინ , თუ , მაშინ ელემენტებს ვარსკვლავით ვნიშნავთ. შემდეგ შედგება წერტილებითა და ვარსკვლავებით მონიშნული ელემენტებისაგან. ეს ნაკრები არ შეიცავს ელემენტს, მაგალითად, . შემდეგ ვაშენებთ სიმრავლეს, რომლის ელემენტებსაც აღვნიშნავთ მარტივი რიცხვით. შემდეგ ის შედგება ელემენტებისაგან, რომლებიც მითითებულია წერტილებით, ვარსკვლავებითა და მარტივი რიცხვებით, მაგრამ არ ემთხვევა . ცხადია, რომ დაემთხვა, აუცილებელია, რომ .

ჩვენ შევქმენით ფაქტორების ნაკრები. ფაქტორიზაციის პროცედურის მიხედვით მიმატების ოპერაცია განისაზღვრება შემდეგნაირად: , სადაც , .

შესავალი 2
1. 4 ჯგუფების განმარტება და მაგალითები
2. ქვეჯგუფები 8
3. ციკლური ჯგუფები. 13
4. ნორმალური გამყოფები, ფაქტორების ჯგუფები 17
5. ქვეჯგუფის იდეალი ჯგუფში. ლაგრანჟის თეორემა და მისგან მიღებული შედეგები. 22
6. ჯგუფების ნორმალური გამყოფების გამოყენება ამოცანების ამოხსნისას 26
დასკვნა 29
გამოყენებული ლიტერატურა 30

შესავალი

უმაღლესი ალგებრა არის დაწყებითი ალგებრის სასკოლო კურსის ძირითადი შინაარსის შორსმიმავალი, მაგრამ საკმაოდ ბუნებრივი განზოგადება. წრფივი ალგებრა, რომელიც არის დიდი მეცნიერება, რომელიც ეძღვნება ძირითადად მატრიცების თეორიას და ვექტორული სივრცეების წრფივი გარდაქმნების თეორიას, ასევე მოიცავს ფორმების თეორიას, ინვარიანტების თეორიას და ტენზორული ალგებრას, რომელიც მნიშვნელოვან როლს ასრულებს დიფერენციალურ გეომეტრიაში. ვექტორული სივრცეების თეორია შემდგომ განვითარებულია ალგებრის გარეთ, ფუნქციონალურ ანალიზში (უსასრულო-განზომილებიანი სივრცეები). მისი გამოყენების მრავალფეროვნებითა და მნიშვნელობით, როგორც მათემატიკაში, ასევე მექანიკაში, ფიზიკასა და ტექნიკურ მეცნიერებებში, წრფივი ალგებრა რჩება პირველ ადგილზე ალგებრის მრავალ დარგს შორის.
ველის თეორია აღმოჩნდა ბუნებრივი არე განტოლებათა თეორიის შემდგომი განვითარებისთვის და მისი ძირითადი განშტოებები - ალგებრული რიცხვების ველების თეორია და ალგებრული ფუნქციის ველების თეორია - აკავშირებდა მას, შესაბამისად, რიცხვთა თეორიასთან და ფუნქციების თეორიასთან. რთული ცვლადის. უმაღლესი ალგებრის კურსი მოიცავს ელემენტარულ შესავალს ველის თეორიაში, ხოლო კურსის ზოგიერთი მონაკვეთი - პოლინომები რამდენიმე უცნობში, მატრიცის ნორმალური ფორმა - დაუყოვნებლივ არის წარმოდგენილი თვითნებური ფუნდამენტური ველის შემთხვევაში.
ველის ცნებაზე უფრო ფართოა ბეჭდის ცნება. ველის შემთხვევისგან განსხვავებით, აქ გაყოფის მიზანშეწონილობა აღარ არის საჭირო და, გარდა ამისა, გამრავლება შეიძლება იყოს არაკომუტაციური და არა ასოციაციურიც კი. რგოლების უმარტივესი მაგალითებია ყველა მთელი რიცხვის სიმრავლე (უარყოფითი რიცხვების ჩათვლით), მრავალწევრების სისტემა ერთ უცნობში და რეალური ცვლადის რეალური ფუნქციების სისტემა. რგოლების თეორია მოიცავს ალგებრის ისეთ ძველ ფილიალებს, როგორიცაა ჰიპერკომპლექსური სისტემების თეორია და იდეალების თეორია, ის ასოცირდება უამრავ მათემატიკურ მეცნიერებასთან / კერძოდ ფუნქციონალურ ანალიზთან და უკვე იპოვა რამდენიმე გამოსავალი ფიზიკაში. უმაღლესი ალგებრის კურსი, არსებითად, შეიცავს მხოლოდ ბეჭდის ცნების განმარტებას.
ჯგუფურ თეორიას აპლიკაციების კიდევ უფრო ფართო სპექტრი აქვს. ჯგუფი არის ალგებრული სისტემა ერთი ძირითადი მოქმედებით და ეს ოპერაცია უნდა იყოს ასოციაციური, თუმცა არა აუცილებლად კომუტაციური და უნდა ჰქონდეს შებრუნებული ოპერაცია - გაყოფა, თუ მთავარ ოპერაციას გამრავლება ჰქვია. ასეთია, მაგალითად, შეკრების მოქმედების მიმართ განხილული მთელი რიცხვების კრებული, ასევე გამრავლების მოქმედებით გათვალისწინებული დადებითი რეალური რიცხვების შეკრება. ჯგუფები უკვე დიდ როლს ასრულებდნენ გალუას თეორიაში, რადიკალებში განტოლებების ამოხსნადობის საკითხში, მაგრამ ახლა ისინი მნიშვნელოვანი ინსტრუმენტია ველის თეორიაში, გეომეტრიის ბევრ დარგში, ტოპოლოგიაში, ისევე როგორც მათემატიკის გარეთ - კრისტალოგრაფიაში. თეორიულ ფიზიკაში. ზოგადად, გამოყენების სფეროს სიგანის თვალსაზრისით, ჯგუფური თეორია ხაზოვანი ალგებრის შემდეგ მეორე ადგილზეა ალგებრის ყველა განშტოებას შორის.
ამ ნაშრომის საგანია ჯგუფების ნორმალური გამყოფები.
Დავალებები:
1. განსაზღვრეთ ჯგუფი და ქვეჯგუფი, განიხილეთ ჯგუფების მაგალითები.
2. განვიხილოთ ციკლური ჯგუფები.
3. განვიხილოთ ნორმალური გამყოფების ცნება
4. მიეცით ლაგრანჟის თეორემა და მისგან შედეგები.
5. განიხილეთ ნორმალური ჯგუფის გამყოფების გამოყენება ამოცანების ამოხსნისას.

გამოყენებული წყაროების სია

1. კულიკოვი ლ.ია. და რიცხვების თეორია: სახელმძღვანელო. სახელმძღვანელო პედაგოგიური ინსტიტუტებისთვის. – : უმაღლესი სკოლა, 1979. – 559გვ., ილ.
2. კოსტრიკინი ა.ი. შესავალი ალგებრაში: სახელმძღვანელო უნივერსიტეტებისთვის. – M.: Fizmatlit, 2004. – 272გვ.
3. ფადეევი დ.კ. ამოცანების კრებული უმაღლეს ალგებრაში. – მ.: ნაუკა, 1977. – 288გვ.
4. კუროშ ა.გ. უმაღლესი ალგებრის კურსი. – მ.: ნაუკა, 1968 წ.
5. ოკუნევი ლ.ია. ამოცანების კრებული უმაღლეს ალგებრაში - მ.: განათლება, 1964 წ.

საერთო მოცულობა: 30 გვ.

წელი: 2013

განმარტებები

ქვეჯგუფი ნჯგუფები გდაურეკა ნორმალური, თუ ის უცვლელია უღლების ქვეშ, ანუ ნებისმიერი ელემენტისთვის ნსაწყისი ნდა ნებისმიერი გსაწყისი გ, ელემენტი გნგ − 1 წევს ნ :

შემდეგი ქვეჯგუფის ნორმალურობის პირობები ექვივალენტურია:

პირობა (1) ლოგიკურად სუსტია ვიდრე (2), ხოლო პირობა (3) ლოგიკურად სუსტია ვიდრე (4). ამიტომ, (1) და (3) პირობები ხშირად გამოიყენება ქვეჯგუფის ნორმალურობის დასადასტურებლად, ხოლო (2) და (4) პირობები გამოიყენება ნორმალურობის შედეგების დასამტკიცებლად.

მაგალითები

• {ე) და გ- ყოველთვის ნორმალური ქვეჯგუფები გ. მათ ტრივიალურს უწოდებენ. თუ სხვა ნორმალური ქვეჯგუფები არ არის, მაშინ ჯგუფი გმარტივი ეწოდება.

• ჯგუფის ცენტრი არის ჩვეულებრივი ქვეჯგუფი.

• ჯგუფის კომუტატორი ჩვეულებრივი ქვეჯგუფია.

• ნებისმიერი დამახასიათებელი ქვეჯგუფი ნორმალურია, რადგან კონიუგაცია ყოველთვის ავტომორფიზმია.

• ყველა ქვეჯგუფი ნაბელიანთა ჯგუფი გნორმალურია, რადგან გნ = ნგ . არააბელიურ ჯგუფს, რომლის ყველა ქვეჯგუფი ნორმალურია, ჰამილტონური ეწოდება.

• პარალელური თარგმანის ჯგუფი ნებისმიერი განზომილების სივრცეში არის ევკლიდური ჯგუფის ნორმალური ქვეჯგუფი; მაგალითად, სამგანზომილებიან სივრცეში როტაცია, თარგმანი და ბრუნვა საპირისპირო მიმართულებით იწვევს მარტივ თარგმნას.

• რუბიკის კუბის ჯგუფში, ქვეჯგუფი, რომელიც შედგება მხოლოდ კუთხის ელემენტებზე მოქმედი ოპერაციებისგან, ნორმალურია, რადგან არანაირი კონიუგატური ტრანსფორმაცია არ გამოიწვევს ამ ოპერაციის მოქმედებას კიდეზე და არა კუთხის ელემენტზე. ამის საპირისპიროდ, ქვეჯგუფი, რომელიც შედგება მხოლოდ ზედა სახის როტაციისგან, არ არის ნორმალური, რადგან თანამოაზრეები აძლევენ ზედა სახის ნაწილების ქვევით გადატანას.

Თვისებები

• ნორმალურობა შენარჩუნებულია სუბიექტური ჰომორფიზმების და ინვერსიული გამოსახულების მიღებისას.
• ნორმალურობა შენარჩუნებულია პირდაპირი პროდუქტის აგებისას.
• ნორმალური ქვეჯგუფის ნორმალური ქვეჯგუფი არ უნდა იყოს ნორმალური ჯგუფში, ანუ ნორმალურობა არ არის გარდამავალი. თუმცა ნორმალური ქვეჯგუფის დამახასიათებელი ქვეჯგუფი ნორმალურია.
• მე-2 ინდექსის ყველა ქვეჯგუფი ნორმალურია. თუ გვ- უმცირესი ძირითადი რიგის გამყოფი გ, შემდეგ ინდექსის ნებისმიერი ქვეჯგუფი გვნორმალური.
• თუ ნ- ნორმალური ქვეჯგუფი გ, შემდეგ მარცხენა (მარჯვნივ) კოსეტების კომპლექტზე გ / ნთქვენ შეგიძლიათ შეხვიდეთ ჯგუფის სტრუქტურაში წესის მიხედვით

(გ 1 ნ)(გ 2 ნ) = (გ 1 გ 2)ნ მიღებულ კომპლექტს ეწოდება ფაქტორების ჯგუფი გავტორი ნ .

• ნნორმალურია, თუ და მხოლოდ იმ შემთხვევაში, თუ ის ტრივიალურად მოქმედებს მარცხენა კოსეტებზე გ / ნ .

ისტორიული ფაქტები

ევარისტ გალუა იყო პირველი, ვინც გაიგო ნორმალური ქვეჯგუფების მნიშვნელობა.

ბმულები

• ვინბერგი ე.ბ.ალგებრის კურსი - მ.: გამომცემლობა Factorial Press, 2002, ISBN 5-88688-060-7

ფონდი ვიკიმედია. 2010 წელი.

• ნორმალური მარკოვის ალგორითმი
• ელექტროდის ნორმალური პოტენციალი

ნახეთ, რა არის „ნორმალური გამყოფი“ სხვა ლექსიკონებში:

ნორმალური გამყოფი- ინვარიანტული ქვეჯგუფი, ჯგუფის თეორიის ერთ-ერთი ძირითადი ცნება (იხ. ჯგუფი), შემოღებული ე.გალუას მიერ. G ჯგუფის N. d. არის H ქვეჯგუფი, რომლისთვისაც gH = Hg G ჯგუფის g ელემენტის ნებისმიერი არჩევანისთვის ... დიდი საბჭოთა ენციკლოპედია

ნორმალური დაყოფა- ნორმალური ქვეჯგუფი, უცვლელი ქვეჯგუფი, G ჯგუფის H ქვეჯგუფი, რომლისთვისაც H ჯგუფის G ჯგუფის მარცხნივ დაშლა H ქვეჯგუფში ემთხვევა მარჯვენა მხარეს, ანუ ისეთ ქვეჯგუფს, რომ ნებისმიერი ელემენტისთვის კოსეტები aH და Ha ტოლია (მნიშვნელობით... ... მათემატიკური ენციკლოპედია

ქვეჯგუფების ნორმალური სერია- ჯგუფის თეორიის ზოგადი აღწერილობისთვის იხილეთ ჯგუფი (მათემატიკა) და ჯგუფის თეორია. დახრილი ასოები მიუთითებს ამ ლექსიკონის მითითებაზე. # A B C D E E F G H I J J K L M N O P R S T U ... ვიკიპედია

ნორმალური რიგი- ჯგუფის თეორიის ზოგადი აღწერილობისთვის იხილეთ ჯგუფი (მათემატიკა) და ჯგუფის თეორია. დახრილი ასოები მიუთითებს ამ ლექსიკონის მითითებაზე. # A B C D E E F G H I J J K L M N O P R S T U ... ვიკიპედია არის ტოპოლოგიური ჯგუფი, კომპაქტური, როგორც ტოპოლოგიური ჯგუფი. სივრცე. მაგალითად, ყველა სასრული ჯგუფი (დისკრეტულ ტოპოლოგიაში) არის ალგებრული ჯგუფი, თუმცა კომპაქტური ტოპოლოგიური ჯგუფია. სივრცე (ზარისკის ტოპოლოგიასთან შედარებით) ... მათემატიკური ენციკლოპედია

ლი - კოლჩინის თეორემა- GL(V) ჯგუფის G ქვეჯგუფს (V არის სასრული განზომილებიანი ვექტორული სივრცე ალგებრულად დახურულ ველზე) აქვს ინდექსის G1 ნორმალური გამყოფი მაქსიმუმ, სადაც p დამოკიდებულია მხოლოდ V-ზე დაბლა, ისეთი, რომ V-ში არის დროშა უცვლელი G1-თან მიმართებაში.…… მათემატიკური ენციკლოპედია

ტოპოლოგიური ჯგუფი- სიმრავლე G, რომელზედაც მოცემულია ორი ჯგუფის სტრუქტურა და ტოპოლოგიური სტრუქტურა. სივრცეები, რომლებიც შეესაბამება ჯგუფური ოპერაციების უწყვეტობის პირობას. კერძოდ, პირდაპირი პროდუქტის G-ში დახატვა უნდა იყოს უწყვეტი. ქვეჯგუფი N T.g.G არის T.g. in... ... მათემატიკური ენციკლოპედია

ლაგრანჟის თეორემა ამბობს, რომ თუ ა
, ეს

იმათ. შეკვეთა
G ჯგუფის ნებისმიერი H ქვეჯგუფი ყოფს N – G ჯგუფის რიგითობას.

ბუნებრივია, ჩნდება კითხვა თეორემის ინვერსიის შესახებ: თუ m არის გამყოფი
, მაშინ G-ს აქვს m რიგის H ქვეჯგუფი?

სხვა სიტყვებით რომ ვთქვათ: N ჯგუფის M რიგის ყოველი გამყოფისთვის, არსებობს თუ არა m რიგის G ჯგუფის H ქვეჯგუფი?

ზოგადად, პასუხი უარყოფითია, მაგრამ ზოგიერთ განსაკუთრებულ შემთხვევაში ეს მიმართვალაგრანჟის თეორემა მართალია.

თეორემა. (ლაგრანჟის თეორემის ინვერსია )

1. ციკლური ჯგუფის ყოველი ქვეჯგუფი ისევ ციკლური ჯგუფია.

2. უსასრულო ციკლური ჯგუფის ქვეჯგუფები

.

3. წესრიგის ციკლური ჯგუფის ქვეჯგუფები ნომრები .

მტკიცებულება.

დავამტკიცოთ 1 . დაე – წესრიგის თვითნებური ციკლური ჯგუფი
. დაზუსტებისთვის, ჩვენ ვივარაუდებთ, რომ - დანამატის ჯგუფი.

ამ შემთხვევაში, ჯგუფის საერთო ელემენტი როგორც ჩანს

დაე
– ჯგუფის თვითნებური არატრივიალური ქვეჯგუფი , ე.ი.
.

იმიტომ რომ
, შემდეგ ქვეჯგუფის ელემენტები
ფორმის ელემენტებია
, მაგრამ თუ.

ფორმის ყველა ელემენტს შორის
აირჩიეთ ელემენტი

, სად
- ყველაზე პატარა დადებითი რიცხვი.

შემდეგ ნებისმიერი
შეიძლება წარმოდგენილი იყოს როგორც:

რისგან

მაგრამ m არის უმცირესი რიცხვი, რომელიც აკმაყოფილებს პირობას

მგH  r = 0  H = ,

იმათ. H არის ციკლური ჯგუფი მგ ფორმირების ელემენტით.

დავამტკიცოთ 2 . უსასრულო ციკლური ჯგუფის ქვეჯგუფები
ამოწურულია უსასრულო ჯგუფებით
.

მართლაც, მას შემდეგ
– ციკლური ჯგუფი გენერატორი ელემენტით 1 ან
, ე.ი.

შემდეგ, ამ თეორემის 1-ლი პუნქტის შესაბამისად, ციკლური ჯგუფის ნებისმიერი H ქვეჯგუფი
განისაზღვრება ნატურალური რიცხვით
და ჰგავს

და ყველა ეს ქვეჯგუფი უსასრულოა.

დავამტკიცოთ 3 . რიგის ციკლური ჯგუფის ქვეჯგუფები არიან ერთერთ შესაბამისობაში დადებით გამყოფებთან ნომრები .

დაე, როგორც ადრე,
– შეკვეთის დანამატი ციკლური ჯგუფი , ე.ი.

თუ და თუ ელემენტი

ჩვენ ეს უნდა დავამტკიცოთ
ყოფს .

მართლაც, წარმოვიდგინოთ

მერე იქიდან რომ

,

და მინიმალურობა
იწვევს
, აქედან გამომდინარე
.

ამრიგად, იქიდან, რომ
, აქედან გამომდინარეობს, რომ ქვეჯგუფი
აქვს წესრიგი , ე.ი.

.

Როდესაც
გადის რიცხვის ყველა დადებით გამყოფზე , იგივეს აკეთებს და მივიღებთ შეკვეთის ზუსტად ერთ ქვეჯგუფს , გამყოფი .

შედეგი. ციკლურ ჯგუფში
შეკვეთა ქვეჯგუფი
შეკვეთა
ემთხვევა ბევრ ელემენტს
, ისეთივე როგორც
.

მტკიცებულება. ციკლური ჯგუფის ელემენტები
შეკვეთა გამოიყურება როგორც

თუ
, ტოი
.

უკან, ნება
და
.

მდგომარეობიდან
ამას მოჰყვება
, სადაც
და.

1. ნორმალური გამყოფები

მოდით G იყოს თვითნებური ჯგუფი და H - G ქვეჯგუფი, მაშინ თუ მივიღებთ ორ მარცხენა კოსეტს.
და
.

ჩვენ გვინდა გავარკვიოთ რა პირობებშია კოსეტებიდან აღებული ელემენტების პროდუქტი
და
, არ არის დამოკიდებული კლასის წარმომადგენლების არჩევანზე და ყოველთვის მიეკუთვნება იმავე კოსეტის კლასს, როგორც ელემენტების პროდუქტი
, კერძოდ კლასი
.

ელემენტი მიეკუთვნება კოზეტების კლასს
და ელემენტი - მიმდებარე კლასი
.

თვითნებური ელემენტები, რომლებიც მიეკუთვნებიან, შესაბამისად, მიმდებარე კლასებს
და
შეიძლება წარმოდგენილი იყოს როგორც:

შემდეგ მათი პროდუქტი

უნდა ეკუთვნოდეს კლასს

.

ეს ნიშნავს, რომ ქვეჯგუფში H,

მარცხენა წევრის მიღებული ტოლობის გამრავლება ნაწილზე , ჩვენ გვაქვს:

(9)

სად

ურთიერთობა (9) საშუალებას გვაძლევს გამოვიტანოთ შემდეგი დასკვნა.

ვინაიდან ელემენტები
არჩეულია თვითნებურად, შემდეგ ნებისმიერი ელემენტისთვის
და ნებისმიერი ელემენტი
არის ელემენტი

,

დამაკმაყოფილებელი ურთიერთობა (9).

გარდა ამისა, ელემენტი
და ელემენტი
. ამის გამო, G ჯგუფის ყველა მარცხენა კოსეტი H-სთან მიმართებაში შეიცავს G ჯგუფის ზოგიერთ მარჯვენა კოსეტს იმავე H ქვეჯგუფთან მიმართებაში:

ანალოგიურად, ჩვენ შეგვიძლია ვაჩვენოთ საპირისპირო ჩართვა

და ეს იმას ნიშნავს

განმარტება 1. G ჯგუფის H ქვეჯგუფს ეწოდება ნორმალური გამყოფიან უცვლელი ქვეჯგუფი, თუ რომელიმე ორი კოსეტისთვის g 1 H და g 2 H ქვეჯგუფში H, პროდუქტი
თვითნებური ელემენტები
ამ კლასებიდან მიეკუთვნება იმავე კოსეტის კლასს
(ნახ. 2).

ბრინჯი. 2– H ქვეჯგუფი არის G ჯგუფის ნორმალური ქვეჯგუფი.

ფორმალურად: ქვეჯგუფი H – ნორმალური გამყოფიჯგუფები , თუ:

კომუტატიურ ჯგუფებში ყველა ქვეჯგუფი არის ნორმალური გამყოფი (შეკრების ოპერაციის კომუტაციური ხასიათის გამო).

ნორმალური გამყოფის კონცეფციის პრაქტიკული გამოყენებისთვის განვიხილოთ კიდევ რამდენიმე „კონსტრუქციული“ განმარტება.

განმარტება 2. G-ის H ქვეჯგუფია ნორმალური გამყოფი G ჯგუფის თუ და მხოლოდ იმ შემთხვევაში, თუ ყველა მარცხენა კოსეტი
ემთხვევა სწორ კოსეტს
ჯგუფები G H-ით და პირიქით.

ფორმალურად: ქვეჯგუფი H – ნორმალური გამყოფიჯგუფი G, თუ:

პირობა (12) აშკარად ნიშნავს, რომ:

მაგალითები.

1. ნებისმიერ G ჯგუფში თავად ჯგუფი
და ერთეული ქვეჯგუფი
არის მისი ნორმალური გამყოფები: G-ის მარცხენა და მარჯვენა კოსეტები ქვეჯგუფების მიხედვით
შედგება ერთი მიმდებარე კლასისგან
, ხოლო H ერთეული ქვეჯგუფის მარცხენა (მარჯვნივ) კოსეტები შედგება G ჯგუფის ყველა ელემენტისგან.

2. ყველა აბელიან ჯგუფში G მისი თითოეული ქვეჯგუფი H არის ნორმალური ქვეჯგუფი.

3. დადებითი რეალური რიცხვების გამრავლების ჯგუფი
არის ყველა არანულოვანი რეალური რიცხვის მრავლობითი ჯგუფის ნორმალური გამყოფი,

4. არანულოვანი რაციონალური რიცხვების მრავლობითი ჯგუფი
არის არანულოვანი რეალური რიცხვების მრავლობითი ჯგუფის ნორმალური გამყოფი

5. გამრავლებით ჯგუფში
არაინგულარული მატრიცები
-მეორე რიგის ქვეჯგუფი რეალური კოეფიციენტებით
მატრიცები, რომელთა განმსაზღვრელი ტოლია ერთი:

არის ამ ჯგუფის ნორმალური გამყოფი.

მართლაც, იდენტურობის მატრიცა
, თუ

და

– შესაბამისად, ჯგუფის მარცხენა და მარჯვენა კოსეტები
-არასიგნორული მატრიცები
-ე რიგით რეალური კოეფიციენტებით ქვეჯგუფზე
- მატრიცები, რომელთა განმსაზღვრელი ტოლია ერთი.

,

იმათ.
.

მეორე მხრივ, თუ

,

იმიტომ რომ
Ამიტომაც

შესაბამისად, თანაბარი განმსაზღვრელი ყველა მატრიცის დაჯგუფებით ერთ კოსეტში (მარცხნივ ან მარჯვნივ) მივიღებთ ჯგუფის დაშლას.
ქვეჯგუფის მიხედვით
. ეს მაგალითი გვიჩვენებს, რომ არაკომუტატიურ ჯგუფებს ასევე შეიძლება ჰქონდეთ ქვეჯგუფები - ნორმალური გამყოფები, რისთვისაც მარცხენა კოსეტი

ემთხვევა სწორ კოსეტს

ქვეჯგუფი ჰჯგუფები გეწოდება ნორმალური გამყოფი, თუ თითოეული ელემენტისთვის გჯგუფები გმისი მარცხენა და მარჯვენა კოსეტები ქვეჯგუფების მიხედვით ჰთანაბარია, ე.ი. გჰ=Hg.

თეორემა 2.5. ქვეჯგუფი ჰჯგუფები გარის ნორმალური გამყოფი, თუ და მხოლოდ იმ შემთხვევაში, თუ იგი შეიცავს ჰნებისმიერისთვის გსაწყისი გდა თსაწყისი ჰ.

მტკიცებულებააშკარად.

დაე ჰარის ჯგუფის ნორმალური გამყოფი გ. კოსეტების სიმრავლეზე წარმოგიდგენთ გამრავლების ოპერაციას, რომელიც გამოწვეულია ჯგუფის ოპერაციით. კოსეტების პროდუქტის ქვეშ აჰდა bHჩვენ გავიგებთ ელემენტების ყველა შესაძლო პროდუქტის კომპლექტს აჰელემენტებზე bH. Იმიტომ რომ ჰარის ნორმალური გამყოფი, მაშინ ყველა ეს პროდუქტი შეიცავს კოსეტის კლასს ( აბ)ჰ. ამრიგად, ოპერაცია დაინერგა კოსეტების კომპლექტზე. ეს ოპერაცია ასოციაციურია ( aHbH)cH=აჰ(bHcH), არის ნეიტრალური ელემენტი ჰდა თითოეული ელემენტისთვის აჰარის საპირისპირო a -1 H. შესაბამისად, კოსეტების კომპლექტი შემოღებულ ოპერაციასთან მიმართებაში ქმნის ჯგუფს, რომელსაც ეწოდება კოეფიციენტური ჯგუფი.

ჯგუფების ჰომორფიზმი.

უნიკალური ჯგუფის ჩვენება გჯგუფს ჰ, რომელიც ინარჩუნებს ოპერაციას, ე.წ ჯგუფური ჰომორფიზმი გვ ჰ.

იზომორფიზმი ჰომორფიზმის განსაკუთრებული შემთხვევაა.

საკუთრება 2.9. ჰომორფიზმის პირობებში, ჯგუფის ნეიტრალური ელემენტი გნაჩვენებია ნეიტრალური ჯგუფის ელემენტში ჰ.

მტკიცებულებათანასწორობიდან გამომდინარეობს.

ჯგუფის მრავალი ელემენტი გნეიტრალურ ელემენტზე გამოსახული, ეწოდება ჰომორფიზმის ბირთვი და აღინიშნება .

საკუთრება 2.10.

მტკიცებულება. Მას შემდეგ.

საკუთრება 2.11. ჰომორფიზმის ბირთვი არის ჯგუფის ნორმალური გამყოფი გ.

მტკიცებულება. ამისთვის ასაწყისი გდა ბბირთვიდან მართალია, ანუ.

ჯგუფის მრავალი ელემენტი ჰ, რომლებიც ელემენტების გამოსახულებებია გ, ეწოდება გამოსახულების ერთობლიობა და აღნიშნავს .

საკუთრება 2.12. სურათების ნაკრები არის ქვეჯგუფი ჰ.

მტკიცებულებააშკარად.

თეორემა 2.6. ფაქტორების ჯგუფი იზომორფულია.

მტკიცებულება. კორესპონდენცია არის ერთი-ერთზე და ინარჩუნებს ოპერაციას, მაშასადამე, იგი განსაზღვრავს იზომორფიზმს და .

თეორემა 2.7. ნებისმიერი ნორმალური გამყოფისთვის ჰჯგუფები გარსებობს ჰომორფიზმი, რომლის ბირთვი ტოლია ჰ. კერძოდ, ასეთი ჰომორფიზმი დან გვ გ/ჰარის .

მტკიცებულებააშკარად.

ნორმალური რიგი

დავამტკიცოთ ორი თეორემა ჰომორფიზმების შესახებ.

თეორემა 2.8. დაე ჰნორმალური ჯგუფის გამყოფი გდა პ- ქვეჯგუფი გ. შემდეგ არის ნორმალური გამყოფი პდა

მტკიცებულება. Იყოს. შემდეგ მას შემდეგ ჰნორმალური გამყოფი გდა რადგან ყველა ელემენტი პ. ამიტომ არის ნორმალური გამყოფი პ. მატჩი არის ერთი-ერთზე და ინარჩუნებს ოპერაციას. თეორემა დადასტურდა.

თეორემა 2.9. დაე პარის ნორმალური გამყოფი და . მერე თ- ნორმალური გამყოფი გდა .

მტკიცებულება. განვიხილოთ სად,. მას შემდეგ, რაც , და ნიშნავს თ- ნორმალური გამყოფი გ. მიმოწერა არის ერთი ერთზე, რადგან და ინახავს ოპერაციას.

ჯგუფს ეწოდება მარტივი, თუ მას არ აქვს ნორმალური გამყოფი, გარდა საკუთარი თავისა და არ აქვს ერთეულების ქვეჯგუფი.

ჯგუფის ნორმალური სერია არის ქვეჯგუფების თანმიმდევრობა, რომელშიც ყოველი მომდევნო არის წინა ჯგუფის ნორმალური გამყოფი. თუ ნორმალური სერიის ყველა ჯგუფი შეიცავს ნორმალურ სერიას, მაშინ მეორე ნორმალური სერიები მიიღება პირველი ნორმალური სერიების კონდენსირებით.

ნორმალურ სერიას გამეორებების გარეშე, რომლის შეკუმშვა შეუძლებელია, ეწოდება კომპოზიციური.

ფაქტორები განისაზღვრება ნორმალური სერიებისთვის . ორ ნორმალურ სერიას იზომორფული ეწოდება, თუ პირველი სერიის ყველა ფაქტორი იზომორფულია მეორე რიგის ფაქტორებთან, რომლებიც გადანაწილებულია გარკვეული თანმიმდევრობით.

საკუთრება 2.13. თუ ნორმალური სერიები იზომორფულია, მაშინ პირველი სერიის თითოეული კონდენსაციისთვის შეგიძლიათ იპოვოთ მეორე სერიის იზომორფული კონდენსაცია.

მტკიცებულება.დავუშვათ, რომ ქვეჯგუფებს შორის გაჩნდა ახალი ქვეჯგუფები. Იმიტომ რომ და, შესაბამისად, ფაქტორები იზომორფულია შესაბამისი ქვეჯგუფების მიმართ. ავღნიშნოთ შესაბამისი ქვეჯგუფით. მოდით განვსაზღვროთ ჯგუფების თანმიმდევრობა, სადაც მე=1,…,ტ. ზემოთ დადასტურებული თეორემის მიხედვით. ამრიგად, მეორე რიგის დატკეპნა ჯგუფების მიხედვით იზომორფულია. ქონება დადასტურდა.