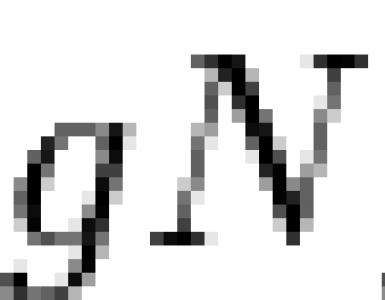Normal gruppdelare. Normalgruppsdelare Normalgruppsdelare

Relaterade klasser. Nedbrytning av en grupp till en undergrupp

Låt vara en grupp, vara dess undergrupp och vara ett godtyckligt element i gruppen. Låt oss göra ett set. Denna icke-tomma uppsättning kallas vänster coset grupper efter undergrupp definierad av elementet. Uppsättningen heter rätt coset grupper efter undergrupp definierad av elementet. I allmänhet.

Problem 61. B hitta höger och vänster coset som definieras av elementet om undergruppen.

Lösning.

Låt oss skapa klasser

Notera, .

Låt vara en grupp och vara dess undergrupp.

Om , då säger de att gruppen för undergrupp är uppdelad i en coset.

Om, så finns det ett element i och då skapar vi en klass.

Om , då sägs gruppen vara uppdelad av undergrupp i två vänster cosets.

Om , då har vi en uppdelning av gruppen i tre coset med avseende på undergruppen, etc.

Processen att sönderdela en grupp till en undergrupp till vänster cosets kan vara ändlig eller oändlig.

På liknande sätt kan vi erhålla en nedbrytning av en grupp efter undergrupp till höger cosets: .

Den högra nedbrytningen behöver inte sammanfalla med den vänstra nedbrytningen.

Som ett resultat får vi två uppsättningar klasser:

Och är de vänstra och högra faktormängderna av mängden för delmängd. Längden på dessa uppsättningar kallas index undergrupper i en grupp.

Problem 62. Hitta faktormängden för en mängd efter undergrupp med avseende på operationen av addition.

Lösning. Operationen för addition till är kommutativ, så vänster- och högerexpansionerna i kommer att vara desamma. Låt oss bryta ner till vänster cosets.

Till exempel, . Vi bygger. . Vi har en nedbrytning i två angränsande klasser. Faktoruppsättning: .

Problem 63. I den multiplikativa gruppen

Låt oss ta en undergrupp. Hitta faktormängden för en mängd med .

Lösning. Med en vänsterexpansion i har vi:

Det vill säga en vänstersidig faktoruppsättning.

Med en högerexpansion i har vi:

Det vill säga en högersidig faktoruppsättning , och , .

Undergruppsindexet i är 3.

Problem 64. Hitta nedbrytningen av additivgruppen i undergruppen av heltal som är multiplar av 3.

Lösning. .

Till exempel, . Låt oss hitta på det. Därför består klassen av alla heltal som när de divideras med 3 lämnar en rest av 1. , till exempel, , . Låt oss hitta på det. Följaktligen består klassen av alla heltal som, när de divideras med 3, lämnar en rest av 2. Så, i är alla de heltal som, när de divideras med 3, lämnar en rest av 0, i klassen är alla heltal som delas med 3, vilket ger in rest 1, i klassen - alla tal med rest 2. Men när de divideras med 3 är bara rester 0, 1, 2 möjliga. Detta innebär att alla heltal är fördelade över klasser, d.v.s. nedbrytning i angränsande klasser av har formen: . Eftersom addition är kommutativ, sammanfaller den vänstra expansionen med den högra expansionen. Undergruppsindexet i är 3.

Normal gruppdelare. Faktorgrupp

Om en grupp har en relativ undergrupp för något element, det vill säga om något element i gruppen pendlar med undergruppen, så kallas undergruppen en normaldelare för gruppen.

Om en operation i en grupp är kommutativ, är varje undergrupp i gruppen en normaldelare. Om, med en vänstersidig och en högersidig nedbrytning av en grupp till en undergrupp, de sammansättningar som gruppen bryts ned i visar sig vara identiska, är det en normaldelare för gruppen. Det omvända är också sant: om är en normaldelare i gruppen, då med en vänstersidig och en högersidig nedbrytning av gruppen till en undergrupp, visar sig de sammansättningar som gruppen delas upp i vara identiska.

Är en normaldelare för en grupp om och endast om för vilket element som helst.

Problem 65. Om undergruppsindexet för en grupp är 2, är gruppens normaldelare.

Lösning. Om en undergrupp har index 2 i gruppen , då , var och , dvs. Följaktligen sammanfaller sammansättningarna av den vänstersidiga sönderdelningen med motsvarande klasser av den högersidiga sönderdelningen, d.v.s. är en normaldelare av gruppen.

Problem 66. Kommer gruppen i uppgift 63 att vara en normaldelare i gruppen?

Lösning. Den vänstra nedbrytningen av en grupp till en undergrupp består av klasserna , och . Den högra nedbrytningen består av klasserna , , , men , , d.v.s. undergruppen är inte en normaldelare av gruppen .

Problem 67. Hitta faktorgruppen för gruppen givet undergruppen av alla tal som är multiplar av 3.

Lösning. Eftersom addition i är kommutativ är det en normaldelare. Låt oss hitta expansionen i: . En faktoruppsättning består av klasser. Låt oss ställa in additionsoperationen:

Att fylla i Cayley-bordet utförs enligt regeln:

Till exempel, . Denna uppsättning består av alla heltal, där, dvs. Sedan . Så vi har erhållit en faktorgrupp, i vilken additionsoperationen ges av den ovan nämnda Cayley-tabellen.

Problem 68. Hitta faktorgruppen för en grupp efter undergrupp.

Lösning.är en normaldelare, eftersom addition i är kommutativ. Låt oss hitta expansionen i: . Låt oss faktiskt avbilda det på nummeraxeln och markera elementen på det med prickar:

Låt oss bygga den där. Om , då , om , då markerar vi elementen med asterisker. Består sedan av element markerade med prickar och asterisker. Denna uppsättning innehåller inte ett element, till exempel . Sedan konstruerar vi en mängd vars element vi betecknar med ett primtal. Sedan består den av element indikerade med punkter, asterisker och primtal, men sammanfaller inte med . Uppenbarligen, för att sammanfalla med , är det nödvändigt att .

Vi har konstruerat en faktoruppsättning. Enligt faktoriseringsproceduren definieras additionsoperationen enligt följande: , där , .

Inledning 2
1. Definition och exempel på grupper 4
2. Undergrupper 8
3. Cykliska grupper. 13
4. Normaldelare, faktorgrupper 17
5. Idealet för en undergrupp inom en grupp. Lagranges sats och konsekvenserna av den. 22
6. Använda normaldelare för grupper när du löser problem 26
Slutsats 29
Referenser 30

Introduktion

Högre algebra är en långtgående, men ganska naturlig generalisering av huvudinnehållet i skolkursen i elementär algebra. Linjär algebra, som är en stor vetenskap som främst ägnas åt teorin om matriser och den relaterade teorin om linjära transformationer av vektorrum, inkluderar också teorin om former, teorin om invarianter och tensoralgebra, som spelar en viktig roll i differentialgeometri. Teorin om vektorrum utvecklas vidare utanför algebra, i funktionsanalys (oändligt dimensionella rum). När det gäller mångfalden och betydelsen av dess tillämpningar både inom matematik och inom mekanik, fysik och tekniska vetenskaper, förblir linjär algebra den första bland de många grenarna av algebra.
Fältteori visade sig vara ett naturligt område för vidareutveckling av ekvationsteorin, och dess huvudgrenar - teorin om algebraiska talfält och teorin om algebraiska funktionsfält - kopplade samman den med talteorin respektive funktionsteorin av en komplex variabel. Den högre algebrakursen innehåller en elementär introduktion till fältteori, och vissa delar av kursen - polynom i flera okända, normalformen av en matris - presenteras omedelbart för fallet med ett godtyckligt grundfält.
Bredare än begreppet ett fält är begreppet en ring. Till skillnad från fallet med ett fält, här krävs inte längre möjligheten till division och dessutom kan multiplikation vara icke-kommutativ och till och med icke-associativ. De enklaste exemplen på ringar är mängden av alla heltal (inklusive negativa), ett system av polynom i en okänd och ett system av reella funktioner av en reell variabel. Ringteori inkluderar sådana gamla grenar av algebra som teorin om hyperkomplexa system och teorin om ideal, den är förknippad med ett antal matematiska vetenskaper / i synnerhet med funktionsanalys, och har redan funnit några utlopp inom fysiken. Förloppet för högre algebra innehåller i huvudsak bara en definition av begreppet en ring.
Gruppteori har ett ännu större tillämpningsområde. En grupp är ett algebraiskt system med en grundläggande operation, och denna operation måste vara associativ, men inte nödvändigtvis kommutativ, och måste ha en invers operation - division, om huvudoperationen kallas multiplikation. Sådan, till exempel, är samlingen av heltal som beaktas med avseende på operationen av addition, såväl som insamlingen av positiva reella tal som beaktas med operationen av multiplikation. Grupper spelade redan en stor roll i Galois-teorin, i frågan om lösbarheten av ekvationer i radikaler, men nu är de ett viktigt verktyg inom fältteorin, inom många grenar av geometri, i topologi, såväl som utanför matematiken - i kristallografi, i teoretisk fysik. Generellt sett, när det gäller bredden av dess tillämpningsområde, rankas gruppteori näst efter linjär algebra bland alla grenar av algebra.
Ämnet för detta arbete är normaldelar av grupper.
Uppgifter:
1. Definiera en grupp och en undergrupp, överväg exempel på grupper.
2. Betrakta cykliska grupper.
3. Tänk på begreppet normaldelare
4. Ge Lagranges sats och konsekvenserna av den.
5. Överväg användningen av normala gruppdelare när du löser problem.

Lista över använda källor

1. Kulikov L.Ya. och tallära: Lärobok. handbok för pedagogiska institut. - : Högre skola, 1979. – 559 s., ill.
2. Kostrikin A.I. Introduktion till algebra: Lärobok för universitet. – M.: Fizmatlit, 2004. – 272 sid.
3. Faddeev D.K. Samling av problem i högre algebra. – M.: Nauka, 1977. – 288 sid.
4. Kurosh A.G. Högre algebrakurs. – M.: Nauka, 1968.
5. Okunev L.Ya. Samling av problem i högre algebra - M.: Education, 1964.

Total volym: 30 s.

År: 2013

Definitioner

Undergrupp N grupper G kallad vanligt, om det är invariant under konjugationer, det vill säga för vilket element som helst n från N och vilka som helst g från G, element gng − 1 ligger i N :

Följande normalitetsförhållanden för undergrupp är ekvivalenta:

Villkor (1) är logiskt svagare än (2) och villkor (3) är logiskt svagare än (4). Därför används ofta villkor (1) och (3) för att bevisa normaliteten för en undergrupp, och villkor (2) och (4) används för att bevisa konsekvenserna av normalitet.

Exempel

• {e) Och G- alltid normala undergrupper G. De kallas triviala. Om det inte finns några andra normala undergrupper, då gruppen G kallas enkel.

• Mitten av gruppen är en normal undergrupp.

• En kommutator i en grupp är en normal undergrupp.

• Vilken som helst karakteristisk undergrupp är normal, eftersom konjugering alltid är en automorfism.

• Alla undergrupper N abelska gruppen Gär normala pga gN = Ng . En icke-abelian grupp vars varje undergrupp är normal kallas Hamiltonian.

• Gruppen av parallella översättningar i ett utrymme av vilken dimension som helst är en normal undergrupp av den euklidiska gruppen; till exempel i tredimensionellt rum leder rotation, translation och rotation i motsatt riktning till en enkel translation.

• I en Rubik's Cube-grupp är en undergrupp som består av operationer som endast verkar på hörnelement normal, eftersom ingen konjugerad transformation skulle få en sådan operation att verka på ett kantelement snarare än ett hörnelement. Däremot är en undergrupp som endast består av rotationer av den övre ytan inte normal, eftersom kompisar tillåter delar av den övre ytan att flyttas nedåt.

Egenskaper

• Normalitet bevaras under surjektiv homomorfismer och att ta omvända bilder.
• Normaliteten bevaras när man konstruerar en direkt produkt.
• En normal undergrupp av en normal undergrupp behöver inte vara normal i gruppen, det vill säga normalitet är inte transitiv. Den karakteristiska undergruppen av en normal undergrupp är dock normal.
• Varje undergrupp av index 2 är normal. Om sid- minsta prime order divisor G, sedan valfri undergrupp av indexet sid vanligt.
• Om N- normal undergrupp i G, sedan på uppsättningen av vänster (höger) cosets G / N du kan ange gruppstrukturen enligt regeln

(g 1 N)(g 2 N) = (g 1 g 2)N Den resulterande mängden kallas en faktorgrupp G Förbi N .

• När normalt om och bara om det verkar trivialt på vänster cosets G / N .

Historiska fakta

Évariste Galois var den första som förstod vikten av normala undergrupper.

Länkar

• Vinberg E.B. Algebrakurs - M.: Factorial Press Publishing House, 2002, ISBN 5-88688-060-7

Wikimedia Foundation. 2010.

• Normal Markov-algoritm
• Normal elektrodpotential

Se vad en "normaldelare" är i andra ordböcker:

Normaldelare- en invariant undergrupp, ett av gruppteorins grundläggande begrepp (Se grupp), introducerat av E. Galois. N.d. i en grupp G är en undergrupp H för vilken gH = Hg för valfritt element g i gruppen G ... Stora sovjetiska encyklopedien

NORMAL INDELNING- en normal undergrupp, en invariant undergrupp, en undergrupp H i gruppen G, för vilken den vänstersidiga nedbrytningen av gruppen G i undergruppen H sammanfaller med den högersidiga, dvs. en undergrupp så att för vilket element som helst cosets aH och Ha är lika (i betydelsen... ... Matematisk uppslagsverk

Normal serie av undergrupper- För en allmän beskrivning av gruppteori, se Grupp (matematik) och Gruppteori. Kursiv stil indikerar en hänvisning till denna ordbok. # A B C D E E F G H I J J K L M N O P R S T U ... Wikipedia

Normal rad- För en allmän beskrivning av gruppteori, se Grupp (matematik) och Gruppteori. Kursiv stil indikerar en hänvisning till denna ordbok. # A B C D E E F G H I J J K L M N O P R S T U ... Wikipedia är en topologisk grupp, kompakt som en topologisk grupp. Plats. Till exempel är varje finit grupp (i en diskret topologi) en algebraisk grupp, även om det är en kompakt topologisk grupp. rymden (i förhållande till Zariski-topologin) ... Matematisk uppslagsverk

LEE - KOLCHINA SAT- en lösbar undergrupp G i gruppen GL(V) (V är ett ändligt dimensionellt vektorrum över ett algebraiskt slutet fält) har en normaldelare G1 av index som mest där p endast beror på dim V, så att det i V finns en flagga invariant med avseende på G1.… … Matematisk uppslagsverk

TOPOLOGISK GRUPP- en mängd G, på vilken två gruppstrukturer och en topologisk struktur ges. utrymmen som överensstämmer med villkoren för kontinuitet i koncernens verksamhet. Mappningen av en direkt produkt till G måste nämligen vara kontinuerlig. Undergrupp N T. g. G är T. g. i... ... Matematisk uppslagsverk

Lagranges sats säger att om , a
, Den där

de där. beställa
vilken undergrupp H som helst i en grupp G delar N – ordningen för gruppen G.

Naturligtvis uppstår frågan om inversionen av satsen: om m är en divisor
, har G då en undergrupp H av ordningen m?

Med andra ord: för varje divisor m av ordningen i grupp N, finns det en undergrupp H av grupp G av ordningen m?

Generellt är svaret negativt, men i vissa speciella fall detta överklagande Lagranges sats är sann.

Sats. (inversion av Lagranges sats )

1. Varje undergrupp i en cyklisk grupp är återigen en cyklisk grupp.

2. Undergrupper av en oändlig cyklisk grupp

.

3. Undergrupper av den cykliska gruppen av ordning tal .

Bevis.

Låt oss bevisa 1 . Låta – godtycklig cyklisk ordningsgrupp
. För visshetens skull kommer vi att anta det – tillsatsgrupp.

I det här fallet, den gemensamma delen av gruppen ser ut som

Låta
– en godtycklig icke-trivial undergrupp av gruppen , dvs.
.

Därför att
, sedan elementen i undergruppen
är delar av formen
, men om.

Bland alla element i formuläret
, välj ett element

, Var
– det minsta positiva talet.

Sedan någon
kan representeras som:

Från vad

men m är det minsta tal som uppfyller villkoret

mgH  r = 0  H = ,

de där. H är en cyklisk grupp med det bildande elementet mg.

Låt oss bevisa 2 . Undergrupper av en oändlig cyklisk grupp
är utmattade av oändliga grupper
.

Faktiskt sedan
– cyklisk grupp med genererande element 1 eller
, dvs.

sedan, i enlighet med stycke 1 i denna sats, varje undergrupp H i den cykliska gruppen
bestäms av ett naturligt tal
och ser ut

och alla dessa undergrupper är oändliga.

Låt oss bevisa 3 . Undergrupper av den cykliska gruppen av ordning är i en-till-en-korrespondens med positiva delare tal .

Låt som tidigare,
– additiv cyklisk grupp av ordning , dvs.

Om och om elementet

Det måste vi bevisa
delar upp .

Sannerligen, låt oss föreställa oss

Sedan från det faktum att

,

och minimalitet
innebär
, därav
.

Alltså från det faktum att
, följer det att undergruppen
har ordning , dvs.

.

När
går igenom alla positiva delare av ett tal , gör samma sak , och vi får exakt en undergrupp av ordning , dela .

Följd. I den cykliska gruppen
beställa undergrupp
beställa
matchar många element
, Så att
.

Bevis. Element i den cykliska gruppen
beställa ser ut som

Om
, toi
.

Tillbaka, låt
Och
.

Från tillståndet
följer det
, var
Och.

1. Normaldelare

Låt G vara en godtycklig grupp och H en undergrupp av G, då om vi får två vänster cosets
Och
.

Vi vill ta reda på under vilka förhållanden produkten av element hämtade från cosets
Och
, beror inte på valet av klassrepresentanter och tillhör alltid samma coset-klass som produkten av element
, nämligen klassen
.

Element tillhör coset-klassen
, och elementet – intilliggande klass
.

Godtyckliga element tillhörande respektive angränsande klasser
Och
kan representeras som:

Sedan deras produkt

måste tillhöra en klass

.

Det betyder att i undergruppen H,

Multiplicera den resulterande jämlikheten på vänster term för term med , vi har:

(9)

Var

Relation (9) tillåter oss att dra följande slutsats.

Eftersom elementen
väljs godtyckligt, sedan för vilket element som helst
och vilket element som helst
det finns ett element

,

tillfredsställande förhållande (9).

Dessutom elementet
och element
. På grund av detta finns varje vänster coset i en grupp G med avseende på H i någon höger coset av en grupp G med avseende på samma undergrupp H:

På samma sätt kan vi visa den omvända inkluderingen

och detta kommer att betyda det

Definition 1. En undergrupp H i en grupp G kallas normaldelare eller invariant undergrupp, om för några två coset g 1 H och g 2 H i undergruppen H, produkten
godtyckliga element
av dessa klasser tillhör samma coset-klass
(Fig. 2).

Ris. 2– Undergrupp H är en normal undergrupp av grupp G.

Formellt: undergrupp H – normaldelare grupper , Om:

I kommutativa grupper är varje undergrupp en normaldelare (på grund av additionsoperationens kommutativa karaktär).

För praktisk användning av begreppet normaldelare, låt oss överväga några mer "konstruktiva i hanteringen" definitioner.

Definition 2. Undergrupp H av G är normaldelare av en grupp G om och endast om varje vänster coset
sammanfaller med rätt coset
grupperna G till H och vice versa.

Formellt: undergrupp H – normaldelare grupp G, om:

Villkor (12) betyder uppenbarligen att:

Exempel.

1. I valfri grupp G gruppen själv
och enhetsundergrupp
är dess normala delare: vänster och höger coset av G efter undergrupp
består av en angränsande klass
, och de vänstra (höger) coseten i enhetsundergruppen H består av alla element i gruppen G.

2. I varje Abelisk grupp G är var och en av dess undergrupper H en normal undergrupp.

3. Multiplikativ grupp av positiva reella tal
är en normaldelare av den multiplikativa gruppen av alla reella tal som inte är noll,

4. Multiplikativ grupp av rationella tal som inte är noll
är en normaldelare av den multiplikativa gruppen av reella tal som inte är noll

5. I en multiplikativ grupp
icke-singularmatriser
-th ordningens undergrupp med reella koefficienter
matriser med determinant lika med ett:

är en normaldelare för denna grupp.

Ja, identitetsmatrisen
, Om

Och

– gruppens vänstra och högra sida
-icke-singularmatriser
-:e ordningen med reella koefficienter över undergruppen
- matriser med determinant lika med ett.

,

De där.
.

Å andra sidan, om

,

eftersom den
Det är därför

Följaktligen, genom att gruppera alla matriser med lika determinanter i en coset (vänster eller höger) får vi uppdelningen av gruppen
efter undergrupp
. Det här exemplet visar att icke-kommutativa grupper också kan ha undergrupper - normaldelare, för vilka den vänstra coseten

sammanfaller med rätt coset

Undergrupp H grupper G kallas en normaldelare om för varje element g grupper G dess vänstra och högra coset efter undergrupp Här lika, dvs. gH=Hg.

Sats 2.5. Undergrupp H grupper Gär en normaldelare om och endast om den ingår i H för alla g från G Och h från H.

Bevis självklart.

Låta Här en normaldelare för en grupp G. På uppsättningen av cosets introducerar vi multiplikationsoperationen som induceras av gruppoperationen. Under produkten av cosets ah Och bH vi kommer att förstå uppsättningen av alla möjliga produkter av element från ah till element bH. Eftersom den Här en normal divisor, så ingår alla dessa produkter i coset-klassen ( ab)H. Således har en operation införts på uppsättningen av tillbehör. Denna operation är associativ ( aHbH)cH=ah(bHcH), finns det ett neutralt element H, och för varje element ah det finns en baksida en -1 H. Följaktligen bildar uppsättningen av cosets med avseende på den introducerade operationen en grupp som kallas en kvotgrupp.

Homomorfism av grupper.

Unik gruppdisplay G till gruppen H, som bevarar driften, kallas grupphomomorfism G V H.

Isomorfism är ett specialfall av homomorfism.

Fastighet 2.9. Under homomorfism, det neutrala elementet i gruppen G visas i det neutrala gruppelementet H.

Bevis följer av jämlikhet.

Många gruppinslag G, mappad till ett neutralt element, kallas homomorfismens kärna och betecknas med .

Fastighet 2.10.

Bevis. Sedan dess.

Fastighet 2.11. Kärnan i homomorfismen är en normaldelare av gruppen G.

Bevis. För a från G Och b från kärnan är sant, det vill säga.

Många gruppinslag H, som är bilder av element G, kallas en uppsättning bilder och betecknar .

Fastighet 2.12. Uppsättningen bilder är en undergrupp H.

Bevis självklart.

Sats 2.6. Faktorgruppen är isomorf.

Bevis. Korrespondensen är en-till-en och bevarar operationen, därför definierar den en isomorfism av och .

Sats 2.7. För alla normaldelare H grupper G det finns en homomorfism vars kärna är lika med H. I synnerhet en sådan homomorfism från G V G/Här .

Bevis självklart.

Normal rad

Låt oss bevisa två satser om homomorfismer.

Sats 2.8. Låta H normal gruppdelare G Och P– undergrupp G. Sedan är normaldelaren P Och

Bevis. Låt det vara. Sedan sedan H normaldelare G, och eftersom alla element från P. Därför är en normaldelare P. Matchen är en-till-en och bevarar driften. Teoremet har bevisats.

Sats 2.9. Låta Pär en normaldelare och . Sedan T– normaldelare G Och .

Bevis. Låt oss överväga var , . Sedan, då, och, betyder T– normaldelare G. Korrespondensen är en-till-en, eftersom och sparar operationen.

En grupp kallas enkel om den inte har någon annan normaldelare än sig själv och ingen enhetsundergrupp.

En normalserie av en grupp är en sekvens av undergrupper där varje efterföljande är en normaldelare av den föregående. Om alla grupper i en normalserie ingår i en normalserie, sägs den andra normalserien erhållas genom att kondensera den första normalserien.

En normal serie utan upprepningar som inte går att komprimera kallas för komposition.

Faktorer definieras för en normal serie . Två normalserier kallas isomorfa om alla faktorer i den första serien är isomorfa till faktorerna i den andra serien omarrangerade i en viss ordning.

Fastighet 2.13. Om normalserier är isomorfa kan man för varje kondensation av den första serien hitta en kondensation av den andra serien som är isomorf till den.

Bevis. Låt oss anta att nya undergrupper har dykt upp mellan undergrupperna. Eftersom den och därför är faktorerna isomorfa för motsvarande undergrupper. Låt oss beteckna med motsvarande undergrupp. Låt oss definiera en sekvens av grupper, var i=1,…,t. Enligt satsen som bevisats ovan. Sålunda är komprimeringen av den andra raden i grupper isomorf. egendom har bevisats.