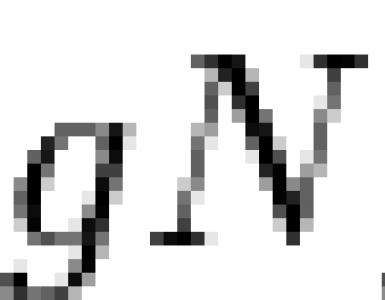Oddiy guruh bo'linuvchisi. Oddiy guruh bo'luvchilari Oddiy guruh bo'luvchilari

Tegishli sinflar. Guruhning kichik guruhga bo'linishi

Guruh bo'lsin, uning kichik guruhi bo'lsin va guruhning ixtiyoriy elementi bo'lsin. Keling, to'plam tuzamiz. Bu bo'sh bo'lmagan to'plam deyiladi chap koset element tomonidan belgilangan kichik guruhlar bo'yicha guruhlar. To'plam deyiladi o'ng koset element tomonidan belgilangan kichik guruhlar bo'yicha guruhlar. Umuman .

Muammo 61. B kichik guruh bo'lsa element tomonidan belgilangan o'ng va chap kosetlarni toping.

Yechim.

Keling, sinflarni yarataylik

Eslatma, .

Guruh bo'lsin va uning kichik guruhi bo'lsin.

Agar bo'lsa, unda ular kichik guruhlar bo'yicha guruh bitta kosetga ajraladi, deyishadi.

Agar, unda element mavjud bo'lsa va keyin biz sinf yaratamiz.

Agar bo'lsa, u holda guruh kichik guruh bo'yicha ikkita chap kosetga ajraladi deyiladi.

Agar bo'lsa, unda biz guruhning kichik guruhga nisbatan uchta kosetga parchalanishiga egamiz va hokazo.

Guruhni kichik guruhga chap kosetlarga ajratish jarayoni chekli yoki cheksiz bo'lishi mumkin.

Xuddi shunday, biz kichik guruhlar bo'yicha guruhning to'g'ri kosetlarga parchalanishini olishimiz mumkin: .

To'g'ri parchalanish chap parchalanish bilan mos kelishi shart emas.

Natijada biz ikkita sinf to'plamini olamiz:

Va pastki to'plam bo'yicha to'plamning chap va o'ng omillar to'plamidir. Ushbu to'plamlarning uzunligi deyiladi indeks guruhdagi kichik guruhlar.

Muammo 62. Qo‘shish amaliga nisbatan kichik guruhlar bo‘yicha to‘plamning omillar to‘plamini toping.

Yechim. Qo'shish amali kommutativdir, shuning uchun chap va o'ng kengaytmalar bir xil bo'ladi. Keling, chap kosetlarga ajratamiz.

Masalan, . Biz quryapmiz. . Bizda ikkita qo'shni sinfga bo'linish mavjud. Faktorlar to'plami: .

Muammo 63. Multiplikativ guruhda

Keling, kichik guruhni olaylik. tomonidan to‘plamning omillar to‘plamini toping.

Yechim. Chap tomonni kengaytirish bilan bizda:

Ya'ni, chap tomonli omillar to'plami.

O'ng tomonni kengaytirish bilan bizda:

Ya'ni, o'ng tomonli koeffitsientlar to'plami , va , .

Kichik guruh indeksi 3 ga teng.

Muammo 64. 3 ga karrali butun sonlar kichik guruhidagi qo‘shimchalar guruhining parchalanishini toping.

Yechim. .

Masalan, . Keling, tuzataylik. Shuning uchun sinf 3 ga bo'linganda 1 qoldig'ini qoldiradigan barcha butun sonlardan iborat. , masalan, , . Keling, tuzataylik. Shunday qilib, sinf 3 ga bo'linganda 2 qoldig'ini qoldiradigan barcha butun sonlardan iborat. Demak, 3 ga bo'linganda 0 qoldig'ini qoldiradigan barcha butun sonlar bo'ladi, sinfdagi barcha bo'lingan butun sonlar. 3 ga, qolgan 1 ni berish, sinfda - qolgan 2 bo'lgan barcha raqamlar. Lekin 3 ga bo'linganda, faqat 0, 1, 2 qoldiqlari mumkin. Bu barcha butun sonlar sinflar bo'ylab taqsimlanadi, ya'ni qo'shni sinflarga parchalanadi. by quyidagi shaklga ega: . Qo'shish kommutativ bo'lgani uchun, chap tomonning kengayishi o'ng qo'lning kengayishi bilan mos keladi. Kichik guruh indeksi 3 ga teng.

Oddiy guruh bo'linuvchisi. Faktorlar guruhi

Agar guruhda har qanday element uchun nisbiy kichik guruh bo'lsa, ya'ni guruhning biron bir elementi kichik guruh bilan almashinadigan bo'lsa, u holda kichik guruh guruhning oddiy bo'luvchisi deb ataladi.

Agar guruhdagi amal kommutativ bo'lsa, u holda guruhdagi har qanday kichik guruh oddiy bo'luvchi hisoblanadi. Agar guruhning chap va o'ng tomonli bo'linishi bilan kichik guruhga bo'linadigan kosetalar bir xil bo'lib chiqsa, u holda guruhning normal bo'luvchisi hisoblanadi. Buning aksi ham to'g'ri: agar guruhda oddiy bo'luvchi bo'lsa, u holda guruhning chap va o'ng tomonli kichik guruhga bo'linishi bilan guruh parchalanadigan kosetalar bir xil bo'lib chiqadi.

Guruhning oddiy bo'luvchisi bo'ladi, agar har qanday element uchun va faqat bo'lsa.

Muammo 65. Agar guruhning kichik guruh indeksi 2 bo'lsa, u holda guruhning normal bo'luvchisi hisoblanadi.

Yechim. Agar kichik guruhda guruhda indeks 2 bo'lsa, u holda, qaerda va, ya'ni. Binobarin, chap tomonlama parchalanishning kosetlari o'ng tomonlama parchalanishning tegishli sinflariga to'g'ri keladi, ya'ni guruhning normal bo'luvchisi hisoblanadi.

Muammo 66. 63-masaladagi guruh guruhda oddiy bo‘luvchi bo‘ladimi?

Yechim. Guruhning kichik guruhga chap tomonida parchalanishi , va sinflardan iborat. O'ng tomondan parchalanish , , , lekin , sinflaridan iborat, ya'ni kichik guruh guruhning oddiy bo'luvchisi emas.

Muammo 67. 3 ga karrali barcha sonlar kichik guruhi berilgan guruhning omil guruhini toping.

Yechim. In qo'shish kommutativ bo'lgani uchun u oddiy bo'luvchidir. Keling, kengaytmani topamiz: . Faktorlar to'plami sinflardan iborat. Qo'shish operatsiyasini o'rnatamiz:

Cayley jadvalini to'ldirish qoidaga muvofiq amalga oshiriladi:

Masalan, . Bu to'plam barcha butun sonlardan iborat bo'lib, bu erda, ya'ni. Keyin. Shunday qilib, biz omil guruhini oldik, unda qo'shish operatsiyasi yuqorida qayd etilgan Keyley jadvali bilan berilgan.

Muammo 68. Kichik guruhlar bo‘yicha guruhning omillar guruhini toping.

Yechim. oddiy boʻluvchidir, chunki in qoʻshilishi kommutativdir. Keling, kengaytmani topamiz: . Darhaqiqat, keling, uni raqamlar o'qida tasvirlaymiz va undagi elementlarni nuqta bilan belgilaymiz:

Keling, uni qayerda quraylik. Agar , keyin , agar , u holda elementlarni yulduzcha bilan belgilaymiz. Keyin nuqta va yulduzcha bilan belgilangan elementlardan iborat. Bu to'plam elementni o'z ichiga olmaydi, masalan, . Keyin biz elementlarini tub bilan belgilaydigan to'plamni tuzamiz. Keyin u nuqta, yulduzcha va tub sonlar bilan ko'rsatilgan elementlardan iborat, lekin bilan mos kelmaydi. Shubhasiz, bilan mos kelish uchun, bu zarur.

Biz omillar to'plamini yaratdik. Faktorlarga ajratish tartibiga ko'ra qo'shish amali quyidagicha aniqlanadi: , bu erda , .

Kirish 2
1. 4-guruhlarning ta’rifi va misollari
2. Kichik guruhlar 8
3. Tsiklik guruhlar. 13
4. Oddiy bo‘luvchilar, omil guruhlari 17
5. Guruh ichidagi kichik guruhning ideali. Lagranj teoremasi va undan kelib chiqadigan natijalar. 22
6. 26-masalalarni yechishda guruhlarning normal bo‘luvchilaridan foydalanish
Xulosa 29
Adabiyotlar 30

Kirish

Oliy algebra - bu boshlang'ich algebra maktab kursining asosiy mazmunini keng qamrovli, ammo juda tabiiy umumlashtirish. Asosan matritsalar nazariyasi va vektor fazolarni chiziqli oʻzgartirish nazariyasiga bagʻishlangan yirik fan boʻlgan chiziqli algebra, shuningdek, differensial geometriyada muhim rol oʻynaydigan shakllar nazariyasi, invariantlar nazariyasi va tenzor algebrasini ham oʻz ichiga oladi. Vektor fazolar nazariyasi algebradan tashqarida, funksional analizda (cheksiz o‘lchovli fazolar) yanada rivojlangan. Matematikada ham, mexanika, fizika va texnika fanlarida ham qo'llanilishining xilma-xilligi va ahamiyati jihatidan chiziqli algebra algebraning ko'plab sohalari orasida birinchi bo'lib qolmoqda.
Maydon nazariyasi tenglamalar nazariyasini yanada rivojlantirish uchun tabiiy soha bo'lib chiqdi va uning asosiy tarmoqlari - algebraik sonlar sohalari nazariyasi va algebraik funktsiyalar sohalari nazariyasi uni mos ravishda raqamlar nazariyasi va funktsiyalar nazariyasi bilan bog'ladi. murakkab o'zgaruvchiga tegishli. Oliy algebra kursi maydon nazariyasiga elementar kirishni o'z ichiga oladi va kursning ba'zi bo'limlari - bir nechta noma'lum ko'phadlar, matritsaning normal shakli - ixtiyoriy fundamental maydon holati uchun darhol taqdim etiladi.
Maydon tushunchasidan kengroq, uzuk tushunchasi. Maydon holatidan farqli o'laroq, bu erda bo'linishning maqsadga muvofiqligi endi talab qilinmaydi va qo'shimcha ravishda, ko'paytirish kommutativ va hatto assotsiativ bo'lmasligi mumkin. Halqalarning eng oddiy misollari - barcha butun sonlar to'plami (shu jumladan manfiylar), bitta noma'lumdagi ko'phadlar tizimi va haqiqiy o'zgaruvchining haqiqiy funktsiyalari tizimi. Ring nazariyasi algebraning giperkompleks tizimlar nazariyasi va ideallar nazariyasi kabi qadimgi tarmoqlarini o'z ichiga oladi, u bir qator matematik fanlar bilan / xususan, funktsional tahlil bilan bog'liq va fizikada ba'zi yo'llarni topdi. Oliy algebra kursi, mohiyatiga ko'ra, faqat halqa tushunchasining ta'rifini o'z ichiga oladi.
Guruh nazariyasi yanada kengroq qo'llash doirasiga ega. Guruh bitta asosiy amalga ega algebraik sistema bo’lib, bu operatsiya assotsiativ bo’lishi kerak, garchi shartli ravishda kommutativ bo’lmasa ham, asosiy amal ko’paytirish deb atalsa, teskari amal – bo’linishga ega bo’lishi kerak. Masalan, qo'shish amaliga nisbatan ko'rib chiqiladigan butun sonlar to'plami, shuningdek, ko'paytirish amali bilan ko'rib chiqiladigan musbat haqiqiy sonlar to'plami. Guruhlar allaqachon Galua nazariyasida, radikallardagi tenglamalarning echilishi masalasida katta rol o'ynagan, ammo hozirda ular maydon nazariyasida, geometriyaning ko'plab sohalarida, topologiyada, shuningdek, matematikadan tashqarida - kristallografiyada, nazariy fizikada. Umuman olganda, qo'llash sohasining kengligi bo'yicha guruh nazariyasi algebraning barcha tarmoqlari orasida chiziqli algebradan keyin keyingi o'rinda turadi.
Ushbu ishning mavzusi guruhlarning oddiy bo'linuvchilari.
Vazifalar:
1. Guruh va kichik guruhni aniqlang, guruhlarga misollar keltiring.
2. Tsiklik guruhlarni ko'rib chiqing.
3. Oddiy bo'luvchilar tushunchasini ko'rib chiqing
4. Lagranj teoremasini va undan chiqadigan natijalarni keltiring.
5. Masalani yechishda oddiy guruh bo’luvchilardan foydalanishni ko’rib chiqing.

Foydalanilgan manbalar ro'yxati

1. Kulikov L.Ya. va sonlar nazariyasi: Darslik. Pedagogika institutlari uchun qo'llanma. – : Yuqori maktab, 1979. - 559 b., kasal.
2. Kostrikin A.I. Algebraga kirish: Universitetlar uchun darslik. – M.: Fizmatlit, 2004. – 272 b.
3. Faddeev D.K. Oliy algebra bo'yicha masalalar to'plami. – M.: Nauka, 1977. – 288 b.
4. Kurosh A.G. Oliy algebra kursi. - M.: Nauka, 1968 yil.
5. Okunev L.Ya. Oliy algebra masalalari toʻplami - M.: Ta'lim, 1964.

Umumiy hajm: 30 bet.

Yil: 2013

Ta'riflar

Kichik guruh N guruhlar G chaqirdi normal, agar u konjugatsiya ostida o'zgarmas bo'lsa, ya'ni har qanday element uchun n dan N va har qanday g dan G, element gng − 1 ichida yotadi N :

Quyidagi kichik guruh normallik shartlari ekvivalentdir:

(1) shart (2) dan mantiqan kuchsiz, (3) shart (4) mantiqan kuchsizroq. Shuning uchun (1) va (3) shartlar ko'pincha kichik guruhning normalligini isbotlashda qo'llaniladi va (2) va (4) shartlar normallik oqibatlarini isbotlash uchun ishlatiladi.

Misollar

• {e) Va G- har doim oddiy kichik guruhlar G. Ular trivial deb ataladi. Agar boshqa oddiy kichik guruhlar bo'lmasa, u holda guruh G oddiy deb ataladi.

• Guruhning markazi oddiy kichik guruhdir.

• Guruhning kommutatori oddiy kichik guruhdir.

• Har qanday xarakterli kichik guruh normaldir, chunki konjugatsiya har doim avtomorfizmdir.

• Barcha kichik guruhlar N abel guruhi G normaldir, chunki gN = Ng . Har bir kichik guruhi normal bo'lgan abel bo'lmagan guruhga Gamiltonian deyiladi.

• Har qanday o'lchamdagi fazodagi parallel tarjimalar guruhi Evklid guruhining oddiy kichik guruhidir; masalan, uch o'lchovli fazoda aylanish, tarjima va teskari yo'nalishda aylanish oddiy tarjimaga olib keladi.

• Rubik kubi guruhida faqat burchak elementlariga ta'sir qiluvchi operatsiyalardan iborat kichik guruh normal hisoblanadi, chunki hech qanday konjugat transformatsiyasi bunday operatsiya burchak elementiga emas, balki chekka elementga ta'sir qilishi mumkin emas. Aksincha, faqat yuqori yuzning aylanishidan iborat kichik guruh normal emas, chunki sheriklar yuqori yuzning qismlarini pastga siljitishga imkon beradi.

Xususiyatlari

• Oddiylik sur'ektiv gomomorfizmlar va teskari tasvirlarni olishda saqlanadi.
• To'g'ridan-to'g'ri mahsulotni qurishda normallik saqlanib qoladi.
• Oddiy kichik guruhning oddiy kichik guruhi guruhda normal bo'lishi shart emas, ya'ni normallik tranzitiv emas. Biroq, oddiy kichik guruhning xarakterli kichik guruhi normaldir.
• Indeks 2 ning har bir kichik guruhi normaldir. Agar p- eng kichik tub tartib bo'luvchi G, keyin indeksning istalgan kichik guruhi p normal.
• Agar N- oddiy kichik guruh G, keyin chap (o'ng) kosetlar to'plamida G / N qoida bo'yicha guruh tuzilishiga kirishingiz mumkin

(g 1 N)(g 2 N) = (g 1 g 2)N Olingan to'plam omillar guruhi deb ataladi G tomonidan N .

• N Agar u chap kosetlarda arzimas harakat qilsagina normal hisoblanadi G / N .

Tarixiy faktlar

Evarist Galois birinchi bo'lib oddiy kichik guruhlarning ahamiyatini tushundi.

Havolalar

• Vinberg E.B. Algebra kursi - M.: Factorial Press nashriyoti, 2002, ISBN 5-88688-060-7

Wikimedia fondi. 2010 yil.

• Oddiy Markov algoritmi
• Oddiy elektrod potentsiali

Boshqa lug'atlarda "Oddiy bo'luvchi" nima ekanligini ko'ring:

Oddiy bo'luvchi- invariant kichik guruh, guruhlar nazariyasining asosiy tushunchalaridan biri (Guruhga qarang), E. Galois tomonidan kiritilgan. G guruhining N. d. - bu H kichik guruhi bo'lib, G guruhining g elementini har qanday tanlash uchun gH = Hg ... Buyuk Sovet Entsiklopediyasi

NORMAL BO'LISH- oddiy kichik guruh, o'zgarmas kichik guruh, G guruhining H kichik guruhi, ular uchun H kichik guruhidagi G guruhining chap tomonli parchalanishi o'ng tomonli bilan mos keladi, ya'ni har qanday element uchun kichik guruh. aH va Ha kosetlari teng (ma'noda ... ... Matematik entsiklopediya

Oddiy kichik guruhlar qatori- Guruh nazariyasining umumiy tavsifi uchun qarang: Guruh (matematika) va Guruh nazariyasi. Kursiv bu lug'atga havolani bildiradi. # A B C D E E F G H I J K L M N O P R S T U ... Vikipediya

Oddiy qator- Guruh nazariyasining umumiy tavsifi uchun qarang: Guruh (matematika) va Guruh nazariyasi. Kursiv bu lug'atga havolani bildiradi. # A B C D E E F G H I J K L M N O P R S T U ... Vikipediya - topologik guruh, topologik guruh sifatida ixcham. bo'sh joy. Misol uchun, har bir chekli guruh (diskret topologiyada) ixcham topologik guruh bo'lsa-da, algebraik guruhdir. fazo (Zariski topologiyasiga nisbatan) ... Matematik entsiklopediya

LI - KOLCHINA TEOREMASI- GL(V) guruhining echiladigan G kichik guruhi (V algebraik yopiq maydon ustidagi chekli o'lchovli vektor fazosi) ko'pi bilan indeksning normal bo'luvchisi G1ga ega bo'ladi, bunda p faqat dim V ga bog'liq, Vda mavjud G1 ga nisbatan bayroq o'zgarmasligi.…… Matematik entsiklopediya

TOPOLOGIK GURUH- ikkita guruh tuzilmasi va topologik tuzilma berilgan G to'plami. guruh operatsiyalarining uzluksizligi shartiga mos keladigan bo'shliqlar. Ya'ni, to'g'ridan-to'g'ri mahsulotni G ga xaritalash uzluksiz bo'lishi kerak. N T. g. G kichik guruhi... ... ichida T.g. Matematik entsiklopediya

Lagranj teoremasi shuni ko'rsatadiki, agar , a
, Bu

bular. buyurtma
G guruhining har qanday H kichik guruhi N bo'linadi - G guruhining tartibi.

Tabiiyki, teoremaning inversiyasi haqida savol tug'iladi: agar m bo'linuvchi bo'lsa.
, u holda G ning m tartibli H kichik guruhi bormi?

Boshqacha qilib aytganda: N guruhning har bir m tartibli bo'luvchisi uchun m tartibli G guruhining H kichik guruhi mavjudmi?

Umuman olganda, javob salbiy, lekin ba'zi maxsus holatlarda bu Shikoyat qilish Lagrange teoremasi haqiqatdir.

Teorema. (Lagranj teoremasining inversiyasi )

1. Siklik guruhning har bir kichik guruhi yana siklik guruhdir.

2. Cheksiz siklik guruhning kichik guruhlari

.

3. Tartibning siklik guruhining kichik guruhlari raqamlar .

Isbot.

Keling, isbot qilaylik 1 . Mayli – tartibning ixtiyoriy siklik guruhi
. Aniqlik uchun biz buni taxmin qilamiz - qo'shimchalar guruhi.

Bunday holda, guruhning umumiy elementi kabi ko'rinadi

Mayli
- guruhning o'zboshimchalik bilan ahamiyatsiz bo'lmagan kichik guruhi , ya'ni.
.

Chunki
, keyin kichik guruhning elementlari
shaklning elementlari hisoblanadi
, lekin agar.

Shaklning barcha elementlari orasida
, elementni tanlang

, Qayerda
- eng kichik ijobiy son.

Keyin har qanday
quyidagicha ifodalanishi mumkin:

Nimadan

lekin m shartni qanoatlantiradigan eng kichik son

mgH  r = 0  H = ,

bular. H - hosil qiluvchi element mg ​​bo'lgan tsiklik guruh.

Keling, isbot qilaylik 2 . Cheksiz tsiklik guruhning kichik guruhlari
cheksiz guruhlar tomonidan charchagan
.

Haqiqatan ham, beri
– generator elementi bo‘lgan siklik guruh yoki
, ya'ni.

keyin ushbu teoremaning 1-bandiga muvofiq, tsiklik guruhning har qanday H kichik guruhi
natural son bilan aniqlanadi
va o'xshaydi

va bu kichik guruhlarning barchasi cheksizdir.

Keling, isbot qilaylik 3 . Tartibning siklik guruhining kichik guruhlari musbat bo'luvchilar bilan birma-bir yozishmalarda bo'ladi raqamlar .

Keling, avvalgidek,
– tartibning qo‘shimcha siklik guruhi , ya'ni.

Agar , va agar element bo'lsa

Biz buni isbotlashimiz kerak
ajratadi .

Haqiqatan ham, tasavvur qilaylik

Keyin bu haqiqatdan

,

va minimallik
nazarda tutadi
, shuning uchun
.

Shunday qilib, bu haqiqatdan
, shundan kelib chiqadiki, kichik guruh
tartib bor , ya'ni.

.

Qachon
sonning barcha musbat bo‘luvchilari orqali o‘tadi , xuddi shu narsani qiladi , va biz buyurtmaning aniq bir kichik guruhini olamiz , bo'lish .

Natija. Tsiklik guruhda
buyurtma kichik guruh
buyurtma
ko'p elementlarga mos keladi
, shu kabi
.

Isbot. Tsiklik guruhning elementlari
buyurtma o'xshamoq

Agar
, toi
.

Orqaga, ruxsat bering
Va
.

Shartdan
shunga amal qiladi
, qayerda
Va.

1. Oddiy bo‘luvchilar

G ixtiyoriy guruh va H G kichik guruhi bo'lsin, agar biz ikkita chap koset olamiz
Va
.

Kosetlardan olingan elementlarning mahsuloti qanday sharoitlarda ekanligini aniqlamoqchimiz
Va
, sinf vakillarini tanlashga bog'liq emas va har doim elementlarning mahsuloti bilan bir xil koset sinfiga tegishli.
, ya'ni sinf
.

Element koset sinfiga kiradi
, va element - qo'shni sinf
.

O'z navbatida, qo'shni sinflarga tegishli bo'lgan ixtiyoriy elementlar
Va
quyidagicha ifodalanishi mumkin:

Keyin ularning mahsuloti

sinfga tegishli bo'lishi kerak

.

Bu shuni anglatadiki, H kichik guruhida,

Chap sondagi hosil bo'lgan tenglikni hadga ko'paytirish , bizda ... bor:

(9)

Qayerda

Munosabatlar (9) quyidagi xulosa chiqarishga imkon beradi.

Elementlardan beri
o'zboshimchalik bilan tanlanadi, keyin har qanday element uchun
va har qanday element
element mavjud

,

qoniqarli munosabat (9).

Bundan tashqari, element
va element
. Shu sababli, H ga nisbatan G guruhining har bir chap kosetasi bir xil H kichik guruhiga nisbatan G guruhining o‘ng kosetida joylashgan:

Xuddi shunday, biz teskari inklyuziyani ko'rsatishimiz mumkin

va bu shuni anglatadi

Ta'rif 1. G guruhining H kichik guruhi deyiladi normal bo'luvchi yoki invariant kichik guruh, H kichik guruhidagi har qanday ikkita koset uchun g 1 H va g 2 H bo'lsa, mahsulot
ixtiyoriy elementlar
bu sinflarning bir xil koset sinfiga tegishli
(2-rasm).

Guruch. 2– H kichik guruhi G guruhining oddiy kichik guruhidir.

Rasmiy ravishda: H kichik guruhi - normal bo'luvchi guruhlar , Agar:

Kommutativ guruhlarda har bir kichik guruh normal bo'luvchidir (qo'shish amalining kommutativ xususiyatidan kelib chiqqan holda).

Oddiy bo'luvchi tushunchasidan amaliy foydalanish uchun keling, yana bir nechta "ishlashda konstruktiv" ta'riflarni ko'rib chiqaylik.

Ta'rif 2. G ning H kichik guruhi normal bo'luvchi G guruhining faqat va faqat har bir chap koset
to'g'ri koset bilan mos keladi
G guruhlari H va aksincha.

Rasmiy ravishda: H kichik guruhi - normal bo'luvchi G guruhi, agar:

Shart (12) aniq shuni anglatadiki:

Misollar.

1. Har qanday G guruhida guruhning o'zi
va birlik kichik guruhi
uning normal bo'luvchilari: kichik guruh bo'yicha G ning chap va o'ng kosetlari
bir qo'shni sinfdan iborat
, va H birlik kichik guruhining chap (o'ng) kosetlari G guruhining barcha elementlaridan iborat.

2. Har bir Abel G guruhida uning har bir kichik guruhi H oddiy kichik guruhdir.

3. Musbat haqiqiy sonlarning multiplikativ guruhi
nolga teng bo'lmagan barcha haqiqiy sonlarning multiplikativ guruhining normal bo'luvchisi,

4. Nolga teng bo'lmagan ratsional sonlarning ko'paytma guruhi
nolga teng bo'lmagan haqiqiy sonlarning ko'paytma guruhining normal bo'luvchisi

5. Multiplikativ guruhda
yagona bo'lmagan matritsalar
-haqiqiy koeffitsientli tartibli kichik guruh
determinanti birga teng bo'lgan matritsalar:

bu guruhning oddiy bo'luvchisidir.

Darhaqiqat, identifikatsiya matritsasi
, Agar

Va

– mos ravishda guruhning chap va o‘ng kosetlari
-singular bo'lmagan matritsalar
-kichik guruh bo'yicha real koeffitsientlarga ega bo'lgan tartib
- determinanti birga teng bo'lgan matritsalar.

,

Bular.
.

Boshqa tomondan, agar

,

chunki
Shunung uchun

Shunday qilib, bir xil determinantli barcha matritsalarni bitta kosetga (chapga yoki o'ngga) guruhlash orqali biz guruhning parchalanishini olamiz.
kichik guruh bo'yicha
. Bu misol shuni ko'rsatadiki, kommutativ bo'lmagan guruhlar ham kichik guruhlarga ega bo'lishi mumkin - oddiy bo'luvchilar, ular uchun chap koset.

to'g'ri koset bilan mos keladi

Kichik guruh H guruhlar G har bir element uchun agar normal bo'luvchi deyiladi g guruhlar G uning chap va o'ng kosetlari kichik guruhlar bo'yicha H teng, ya'ni. gH=Hg.

2.5 teorema. Kichik guruh H guruhlar G tarkibida bo'lsa, oddiy bo'luvchi hisoblanadi H har qanday uchun g dan G Va h dan H.

Isbot aniq.

Mayli H guruhning oddiy bo‘luvchisidir G. Kosetlar to'plamida biz guruh operatsiyasi bilan induktsiya qilingan ko'paytirish amalini kiritamiz. Kosets mahsuloti ostida aH Va bH dan elementlarning barcha mumkin bo'lgan mahsulotlar to'plamini tushunamiz aH elementlarga bH. Chunki H oddiy bo'luvchi bo'lsa, bu mahsulotlarning barchasi koset sinfiga kiradi ( ab)H. Shunday qilib, kosetalar to'plamida operatsiya joriy etildi. Bu operatsiya assotsiativ ( aHbH)cH=aH(bHcH), neytral element mavjud H, va har bir element uchun aH teskarisi bor a -1H. Binobarin, kiritilgan operatsiyaga nisbatan kosetalar to'plami ko'rsatkichlar guruhi deb ataladigan guruhni tashkil qiladi.

Guruhlarning gomomorfizmi.

Noyob guruh ekrani G guruhga H operatsiyani saqlaydigan , deyiladi guruh gomomorfizmi G V H.

Izomorfizm gomomorfizmning alohida holatidir.

Mulk 2.9. Gomomorfizm ostida guruhning neytral elementi G neytral guruh elementida ko'rsatiladi H.

Isbot tenglikdan kelib chiqadi.

Ko'p guruh elementlari G, neytral element bilan tasvirlangan, gomomorfizmning yadrosi deb ataladi va bilan belgilanadi.

Mulk 2.10.

Isbot. O'shandan beri.

Mulk 2.11. Gomomorfizmning yadrosi guruhning oddiy bo'luvchisidir G.

Isbot. Uchun a dan G Va b asosiydan to'g'ri, ya'ni.

Ko'p guruh elementlari H, bu elementlarning tasvirlari G, tasvirlar to'plami deb ataladi va bildiradi.

Mulk 2.12. Rasmlar to'plami kichik guruhdir H.

Isbot aniq.

2.6 teorema. Faktorlar guruhi izomorfdir.

Isbot. Muvofiqlik yakkama-yakka va amalni saqlab qoladi, shuning uchun u va ning izomorfizmini belgilaydi.

2.7 teorema. Har qanday oddiy bo'luvchi uchun H guruhlar G yadrosi teng bo'lgan gomomorfizm mavjud H. Xususan, dan bunday gomomorfizm G V G/H hisoblanadi .

Isbot aniq.

Oddiy qator

Keling, gomomorfizm haqidagi ikkita teoremani isbotlaylik.

2.8 teorema. Mayli H normal guruh bo'luvchisi G Va P- kichik guruh G. Keyin oddiy bo'luvchi P Va

Isbot. Tinch qo'y, hamma narsa o'z holidagiday qo'sin; shunday bo'lsin. O'shandan beri H normal bo'luvchi G, va barcha elementlardan beri P. Shuning uchun u oddiy bo'luvchidir P. Gugurt birma-bir bo'lib, operatsiyani saqlaydi. Teorema isbotlangan.

2.9 teorema. Mayli P oddiy bo'luvchidir va . Keyin T- normal bo'luvchi G Va .

Isbot. Keling, qaerda ekanligini ko'rib chiqaylik. dan beri, keyin, va, degan ma’noni anglatadi T- normal bo'luvchi G. Muloqot birma-bir, chunki va operatsiyani saqlaydi.

Guruhning o'zidan boshqa oddiy bo'luvchisi va birlik kichik guruhi bo'lmasa, oddiy deyiladi.

Guruhning normal qatori - har bir keyingi guruh avvalgisining normal bo'luvchisi bo'lgan kichik guruhlar ketma-ketligi. Agar normal qatorning barcha guruhlari normal qatorda bo'lsa, ikkinchi normal qator birinchi normal qatorni zichlash orqali olinadi.

Siqilib bo'lmaydigan takroriy ketma-ketliklar kompozitsion deyiladi.

Oddiy qator uchun omillar aniqlanadi . Ikki oddiy qator izomorf deyiladi, agar birinchi qatorning barcha omillari ma'lum bir tartibda qayta joylashtirilgan ikkinchi qator omillariga izomorf bo'lsa.

Mulk 2.13. Agar normal qatorlar izomorf bo'lsa, birinchi qatorning har bir kondensatsiyasi uchun unga izomorf bo'lgan ikkinchi qatorning kondensatsiyasini topish mumkin.

Isbot. Faraz qilaylik, kichik guruhlar o'rtasida yangi kichik guruhlar paydo bo'ldi. Chunki va shuning uchun omillar mos keladigan kichik guruhlar uchun izomorfdir. Tegishli kichik guruh bilan belgilaymiz. Keling, guruhlar ketma-ketligini aniqlaymiz, bu erda i=1,…,t. Yuqorida isbotlangan teorema bo'yicha. Shunday qilib, ikkinchi qatorning guruhlar bo'yicha siqilishi izomorfdir. mulki isbotlangan.