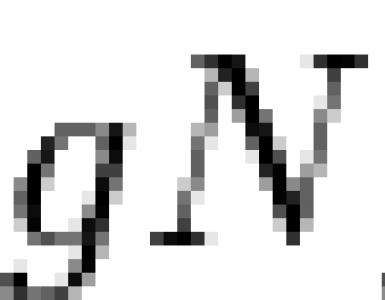مقسم المجموعة العادي. مقسوم المجموعة العادية مقسوم المجموعة العادية

الطبقات ذات الصلة. تحلل المجموعة إلى مجموعة فرعية

دع المجموعة تكون مجموعتها الفرعية وتكون عنصرًا تعسفيًا في المجموعة. دعونا نجعل مجموعة. تسمى هذه المجموعة غير الفارغة كوزيت الأيسرالمجموعات حسب المجموعة الفرعية المحددة بواسطة العنصر. المجموعة تسمى مجموعة الحقالمجموعات حسب المجموعة الفرعية المحددة بواسطة العنصر. على العموم .

المشكلة 61.ب ابحث عن مجموعتي التمام اليمنى واليسرى المحددة بواسطة العنصر إذا كانت المجموعة الفرعية .

حل.

دعونا إنشاء الطبقات

ملحوظة، .

اسمحوا أن تكون مجموعة وتكون مجموعتها الفرعية.

إذا، فإنهم يقولون إن المجموعة حسب المجموعة الفرعية مقسمة إلى مجموعة كاملة واحدة.

إذا كان هناك عنصر ثم سنقوم بإنشاء فئة.

إذا، يقال أن المجموعة مقسمة بواسطة مجموعة فرعية إلى مجموعتين على اليسار.

إذا كان لدينا تحليل المجموعة إلى ثلاث مجموعات فيما يتعلق بالمجموعة الفرعية، وما إلى ذلك.

يمكن أن تكون عملية تحليل مجموعة إلى مجموعة فرعية إلى مجموعات كاملة على اليسار محدودة أو لا نهائية.

وبالمثل، يمكننا الحصول على تحليل مجموعة حسب المجموعة الفرعية إلى مجموعات صحيحة: .

وليس من الضروري أن يتزامن التحلل الأيمن مع التحلل الأيسر.

ونتيجة لذلك، نحصل على مجموعتين من الطبقات:

وهي مجموعات العوامل اليمنى واليسرى للمجموعة حسب المجموعة الفرعية. طول هذه المجموعات يسمى فِهرِسمجموعات فرعية في المجموعة.

المشكلة 62.أوجد مجموعة العوامل لمجموعة فرعية فيما يتعلق بعملية الجمع.

حل.عملية الإضافة إلى هي عملية تبادلية، وبالتالي فإن التوسعات اليمنى واليسرى ستكون هي نفسها. دعونا تتحلل إلى مجموعات اليسار.

على سبيل المثال، . نحن نبني. . لدينا تحلل إلى فئتين متجاورتين. مجموعة العوامل: .

المشكلة 63.في المجموعة الضربية

لنأخذ مجموعة فرعية. أوجد مجموعة العوامل لمجموعة بواسطة .

حل.مع التوسع الأيسر لدينا:

وهذا هو، مجموعة العوامل من الجانب الأيسر.

مع التوسع الأيمن لدينا:

وهذا هو، مجموعة عوامل الجانب الأيمن، و .

فهرس المجموعة الفرعية هو 3.

المشكلة 64.أوجد تحليل المجموعة المضافة في المجموعة الفرعية للأعداد الصحيحة التي تكون مضاعفات العدد 3.

حل. .

على سبيل المثال، . دعونا نجعل الأمر. لذلك، يتكون الفصل من جميع الأعداد الصحيحة التي عند قسمتها على 3 يترك الباقي 1. على سبيل المثال، . دعونا نجعل الأمر. وبالتالي، تتكون الفئة من جميع الأعداد الصحيحة التي عند قسمتها على 3، تترك الباقي 2. إذن، هي جميع الأعداد الصحيحة التي عندما تقسم على 3، تترك الباقي 0، في الفئة هي جميع الأعداد الصحيحة التي يتم قسمتها على 3، مع إعطاء الباقي 1، في الفصل - جميع الأرقام مع الباقي 2. ولكن عند القسمة على 3، تكون البقايا 0، 1، 2 فقط ممكنة، وهذا يعني أن جميع الأعداد الصحيحة يتم توزيعها عبر الفئات، أي التحلل إلى فئات مجاورة بواسطة لديه النموذج: . بما أن عملية الجمع هي عملية تبادلية، فإن المفكوك الأيسر يتزامن مع المفكوك الأيمن. فهرس المجموعة الفرعية هو 3.

مقسم المجموعة العادي. مجموعة العوامل

إذا كانت المجموعة تحتوي على مجموعة فرعية نسبية لأي عنصر، أي إذا كان أي عنصر من المجموعة ينتقل مع المجموعة الفرعية، فإن المجموعة الفرعية تسمى المقسوم العادي للمجموعة.

إذا كانت العملية في المجموعة عبارة عن عملية تبادلية، فإن أي مجموعة فرعية في المجموعة تعتبر مقسومًا عاديًا. إذا، مع التحلل من الجانب الأيسر والأيمن لمجموعة إلى مجموعة فرعية، فإن المجموعات التي تتحلل إليها المجموعة تكون متطابقة، عندها يكون المقسوم عليه طبيعيًا للمجموعة. والعكس صحيح أيضًا: إذا كان المقسوم عليه عاديًا في المجموعة، فعند التحلل من الجانب الأيسر والأيمن للمجموعة إلى مجموعة فرعية، فإن المجموعات التي تتحلل إليها المجموعة تكون متطابقة.

هو المقسوم العادي لمجموعة إذا وفقط إذا لأي وأي عنصر.

المشكلة 65.إذا كان فهرس المجموعة الفرعية للمجموعة هو 2، فهذا هو المقسوم العادي للمجموعة.

حل.إذا كانت المجموعة الفرعية تحتوي على فهرس 2 في المجموعة، إذن، أين و، على سبيل المثال. وبالتالي، فإن مجموعات التحلل على الجانب الأيسر تتزامن مع الفئات المقابلة للتحلل على الجانب الأيمن، أي أنها مقسومة طبيعية على المجموعة.

المشكلة 66.هل ستكون المجموعة في المسألة 63 مقسومًا عاديًا على المجموعة؟

حل.يتكون تحليل الجانب الأيسر من المجموعة إلى مجموعة فرعية من الفئات و . يتكون التحلل الأيمن من الفئات، و، ولكن،، أي أن المجموعة الفرعية ليست مقسومًا عاديًا على المجموعة.

المشكلة 67.أوجد مجموعة عوامل المجموعة بمعلومية المجموعة الفرعية لجميع الأعداد من مضاعفات العدد 3.

حل.وبما أن عملية الجمع هي عملية تبادلية، فهي مقسومة عادية. لنجد التوسعة في : . مجموعة العوامل تتكون من فئات. لنقم بتعيين عملية الإضافة:

يتم ملء جدول كايلي وفقًا للقاعدة:

على سبيل المثال، . تتكون هذه المجموعة من جميع الأعداد الصحيحة، حيث، على سبيل المثال، . ثم . وبذلك نكون قد حصلنا على مجموعة عوامل، عملية الجمع التي يعطى فيها جدول كايلي المذكور أعلاه.

المشكلة 68.أوجد مجموعة العوامل لمجموعة حسب المجموعة الفرعية.

حل.هو مقسوم عادي، لأن الجمع هو إبدالي. لنجد التوسعة في : . وبالفعل، فلنرسمه على محور الأعداد، ونحدد العناصر الموجودة عليه بالنقاط:

دعونا نبنيها حيث. إذا، إذن، إذا، فإننا نضع علامة على العناصر بالنجمة. ثم يتكون من العناصر المميزة بالنقاط والعلامات النجمية. لا تتضمن هذه المجموعة عنصرًا، على سبيل المثال، . ثم نقوم ببناء مجموعة نشير إلى عناصرها بأعداد أولية. ثم يتكون من عناصر يشار إليها بالنقاط والنجمة والأعداد الأولية، ولكنها لا تتطابق مع . ومن الواضح أنه لكي يتزامن مع ذلك، فمن الضروري أن .

لقد قمنا ببناء مجموعة العوامل. وفقا لإجراءات التحليل، يتم تعريف عملية الجمع على النحو التالي: ، حيث، .

مقدمة 2
1. تعريف وأمثلة على المجموعات 4
2. المجموعات الفرعية 8
3. المجموعات الدورية. 13
4. المقسومات العادية، مجموعات العوامل 17
5. المثل الأعلى للمجموعة الفرعية داخل المجموعة. نظرية لاغرانج والنتائج المترتبة عليها. 22
6. استخدام المقسومات الطبيعية للمجموعات عند حل المسائل 26
الاستنتاج 29
المراجع 30

مقدمة

الجبر العالي هو تعميم بعيد المدى ولكنه طبيعي تمامًا للمحتوى الرئيسي للدورة المدرسية للجبر الابتدائي. الجبر الخطي، وهو علم كبير مخصص بشكل أساسي لنظرية المصفوفات والنظرية ذات الصلة بالتحولات الخطية للفضاءات المتجهة، يتضمن أيضًا نظرية الأشكال ونظرية الثوابت والجبر الموتر، الذي يلعب دورًا مهمًا في الهندسة التفاضلية. تم تطوير نظرية الفضاءات المتجهة بشكل أكبر خارج الجبر، في التحليل الوظيفي (الفضاءات اللانهائية الأبعاد). ومن حيث تنوع وأهمية تطبيقاته في كل من الرياضيات والميكانيكا والفيزياء والعلوم التقنية، يظل الجبر الخطي هو الأول بين فروع الجبر العديدة.
تحولت نظرية المجال إلى مجال طبيعي لمزيد من التطوير لنظرية المعادلات، وفروعها الرئيسية - نظرية حقول الأعداد الجبرية ونظرية مجالات الدوال الجبرية - ربطتها، على التوالي، بنظرية الأعداد ونظرية الدوال من متغير معقد. تشتمل دورة الجبر العالي على مقدمة أولية لنظرية المجال، ويتم عرض بعض أقسام الدورة - متعددات الحدود في عدة مجاهيل، الشكل الطبيعي للمصفوفة - على الفور في حالة المجال الأساسي التعسفي.
أوسع من مفهوم المجال هو مفهوم الحلقة. على عكس حالة الحقل، هنا لم تعد جدوى القسمة مطلوبة، وبالإضافة إلى ذلك، يمكن أن يكون الضرب غير تبادلي وحتى غير ترابطي. أبسط الأمثلة على الحلقات هي مجموعة الأعداد الصحيحة (بما في ذلك الأعداد السالبة)، ونظام كثيرات الحدود في مجهول واحد، ونظام الوظائف الحقيقية لمتغير حقيقي. تتضمن نظرية الحلقة فروعًا قديمة من الجبر مثل نظرية الأنظمة فائقة التعقيد ونظرية المُثُل، وترتبط بعدد من العلوم الرياضية / على وجه الخصوص بالتحليل الوظيفي، وقد وجدت بالفعل بعض المنافذ في الفيزياء. مسار الجبر العالي، في جوهره، يحتوي فقط على تعريف لمفهوم الحلقة.
نظرية المجموعة لديها مجموعة أكبر من التطبيقات. المجموعة عبارة عن نظام جبري له عملية أساسية واحدة، ويجب أن تكون هذه العملية ترابطية، وإن لم تكن بالضرورة تبادلية، ويجب أن يكون لها عملية عكسية - القسمة، إذا كانت العملية الرئيسية تسمى الضرب. مثل، على سبيل المثال، مجموعة الأعداد الصحيحة التي يتم النظر فيها فيما يتعلق بعملية الجمع، وكذلك مجموعة الأعداد الحقيقية الموجبة التي يتم النظر فيها في عملية الضرب. لعبت المجموعات بالفعل دورًا كبيرًا في نظرية جالوا، في مسألة قابلية حل المعادلات في الجذور، لكنها الآن أداة مهمة في نظرية المجال، في العديد من فروع الهندسة، في الطوبولوجيا، وكذلك خارج الرياضيات - في علم البلورات، في الفيزياء النظرية. بشكل عام، من حيث اتساع مجال تطبيقاتها، تحتل نظرية المجموعات المرتبة التالية بعد الجبر الخطي بين جميع فروع الجبر.
موضوع هذا العمل هو المقسومات العادية للمجموعات.
مهام:
1. حدد مجموعة ومجموعة فرعية، وفكر في أمثلة للمجموعات.
2. النظر في المجموعات الدورية.
3. النظر في مفهوم المقسومات العادية
4. إعطاء نظرية لاغرانج والنتائج المترتبة عليها.
5. النظر في استخدام مقسومات المجموعة العادية عند حل المسائل.

قائمة المصادر المستخدمة

1. كوليكوف إل.يا. ونظرية الأعداد: كتاب مدرسي. دليل للمعاهد التربوية. – : أعلى المدرسة، 1979. - 559 ص، مريض.
2. كوستريكين أ. مقدمة في الجبر: كتاب مدرسي للجامعات. – م: فيزماتليت، 2004. – 272 ص.
3. فاديف د.ك. مجموعة من المشاكل في الجبر العالي. – م: ناوكا، 1977. – 288 ص.
4. كوروش أ.ج. دورة الجبر العالي. - م: ناوكا، 1968.
5. أوكونيف إل.يا. مجموعة مشاكل في الجبر العالي - م: التربية، 1964.

الحجم الإجمالي: 30 ص.

سنة: 2013

تعريفات

مجموعة فرعية نمجموعات زمُسَمًّى طبيعي، إذا كان ثابتًا في ظل الإقتران، أي لأي عنصر نمن نوأي زمن ز، عنصر زنز − 1 تقع في ن :

الظروف الطبيعية للمجموعة الفرعية التالية متكافئة:

الشرط (1) أضعف منطقيا من (2)، والشرط (3) أضعف منطقيا من (4). لذلك، غالبًا ما يتم استخدام الشرطين (1) و (3) عند إثبات الحالة الطبيعية لمجموعة فرعية، ويتم استخدام الشرطين (2) و (4) لإثبات نتائج الحالة الطبيعية.

أمثلة

• {ه) و ز- مجموعات فرعية عادية دائمًا ز. يطلق عليهم تافهة. إذا لم تكن هناك مجموعات فرعية عادية أخرى، ثم المجموعة زيسمى بسيط.

• مركز المجموعة هو مجموعة فرعية عادية.

• عاكس المجموعة هو مجموعة فرعية عادية.

• تعتبر أي مجموعة فرعية مميزة أمرًا طبيعيًا، نظرًا لأن الاقتران دائمًا ما يكون ذاتيًا.

• جميع المجموعات الفرعية نمجموعة أبيليان زطبيعية بسبب زن = نز . المجموعة غير الأبيلية التي تكون كل مجموعة فرعية فيها طبيعية تسمى هاميلتونية.

• مجموعة الترجمات المتوازية في الفضاء من أي بعد هي مجموعة فرعية عادية من المجموعة الإقليدية؛ على سبيل المثال، في الفضاء ثلاثي الأبعاد، يؤدي التدوير والترجمة والدوران في الاتجاه المعاكس إلى ترجمة بسيطة.

• في مجموعة مكعبات روبيك، من الطبيعي وجود مجموعة فرعية تتكون من عمليات تعمل على عناصر الزاوية فقط، نظرًا لعدم وجود تحويل مترافق قد يتسبب في عمل مثل هذه العملية على عنصر حافة بدلاً من عنصر زاوية. في المقابل، فإن المجموعة الفرعية التي تتكون فقط من دوران الوجه العلوي ليست طبيعية، حيث أن الرفاق يسمحون بتحريك أجزاء من الوجه العلوي إلى الأسفل.

ملكيات

• يتم الحفاظ على الحياة الطبيعية في ظل التماثلات الشمولية والتقاط صور معكوسة.
• يتم الحفاظ على الحالة الطبيعية عند بناء منتج مباشر.
• لا يجب أن تكون المجموعة الفرعية العادية لمجموعة فرعية عادية طبيعية في المجموعة، أي أن الحالة الطبيعية ليست متعدية. ومع ذلك، فإن المجموعة الفرعية المميزة للمجموعة الفرعية العادية هي مجموعة طبيعية.
• كل مجموعة فرعية من الفهرس 2 طبيعية. لو ص- أصغر مقسوم على الرتبة الأولية ز، ثم أي مجموعة فرعية من الفهرس صطبيعي.
• لو ن- مجموعة فرعية عادية في ز، ثم على مجموعة المجموعات اليسرى (اليمنى). ز / نيمكنك الدخول إلى هيكل المجموعة وفقًا للقاعدة

(ز 1 ن)(ز 2 ن) = (ز 1 ز 2)ن المجموعة الناتجة تسمى مجموعة العوامل زبواسطة ن .

• نيعد أمرًا طبيعيًا إذا وفقط إذا كان يعمل بشكل تافه على المجموعات اليسرى ز / ن .

حقائق تاريخية

كان إيفاريست جالوا أول من فهم أهمية المجموعات الفرعية الطبيعية.

روابط

• فينبرج إي.بي.دورة الجبر - م.: دار النشر الصحفية المعملية، 2002، ISBN 5-88688-060-7

مؤسسة ويكيميديا. 2010.

• خوارزمية ماركوف العادية
• إمكانات القطب الطبيعي

انظر ما هو "المقسوم عليه العادي" في القواميس الأخرى:

المقسوم عليه عادي- مجموعة فرعية ثابتة، أحد المفاهيم الأساسية لنظرية المجموعة (انظر المجموعة)، قدمها E. Galois. N. d. للمجموعة G هي مجموعة فرعية H حيث gH = Hg لأي اختيار للعنصر g من المجموعة G ... الموسوعة السوفيتية الكبرى

القسمة العادية- مجموعة فرعية عادية، مجموعة فرعية ثابتة، مجموعة فرعية H من المجموعة G، حيث يتزامن تحلل الجانب الأيسر للمجموعة G في المجموعة الفرعية H مع الجانب الأيمن، أي مجموعة فرعية بحيث يكون لأي عنصر cosets aH و Ha متساويان (بمعنى... ... الموسوعة الرياضية

سلسلة عادية من المجموعات الفرعية- للحصول على وصف عام لنظرية المجموعة، انظر المجموعة (الرياضيات) ونظرية المجموعة. تشير الخطوط المائلة إلى إشارة إلى هذا القاموس. # A B C D E E F G H I J J K L M N O P R S T U ... ويكيبيديا

صف عادي- للحصول على وصف عام لنظرية المجموعة، انظر المجموعة (الرياضيات) ونظرية المجموعة. تشير الخطوط المائلة إلى إشارة إلى هذا القاموس. # A B C D E E F G H I J J K L M N O P R S T U ... ويكيبيديا هي مجموعة طوبولوجية مدمجة كمجموعة طوبولوجية. فضاء. على سبيل المثال، كل مجموعة منتهية (في طوبولوجيا منفصلة) هي مجموعة جبرية، على الرغم من أنها مجموعة طوبولوجية مدمجة. الفضاء (نسبة إلى طوبولوجيا زاريسكي) ... الموسوعة الرياضية

لي - نظرية كولتشينا- مجموعة فرعية قابلة للحل G من المجموعة GL(V) (V هي مساحة متجهة محدودة الأبعاد فوق حقل مغلق جبريًا) لها مقسوم عادي G1 للمؤشر على الأكثر حيث p يعتمد فقط على dim V، بحيث يوجد في V علم ثابت فيما يتعلق بـ G1.… ... الموسوعة الرياضية

المجموعة الطوبولوجية- مجموعة G، والتي يتم فيها إعطاء هيكلين جماعيين وبنية طوبولوجية. المساحات المتوافقة مع شرط استمرارية عمليات المجموعة. أي أن تعيين المنتج المباشر إلى G يجب أن يكون مستمرًا. المجموعة الفرعية N T. g. G هي T. g. في... ... الموسوعة الرياضية

تنص نظرية لاغرانج على أنه إذا كان أ
، الذي - التي

أولئك. طلب
أي مجموعة فرعية H من المجموعة G تقسم N - ترتيب المجموعة G.

بطبيعة الحال، يطرح السؤال حول انقلاب النظرية: إذا كان m مقسومًا عليه
، فهل لدى G مجموعة فرعية H من الرتبة m؟

بمعنى آخر: لكل مقسوم m من رتبة المجموعة N، هل توجد مجموعة فرعية H من المجموعة G من رتبة m؟

بشكل عام، الجواب سلبي، ولكن في بعض الحالات الخاصة هذا جاذبيةنظرية لاغرانج صحيحة.

نظرية. (قلب نظرية لاغرانج )

1. كل مجموعة فرعية من مجموعة دائرية هي مرة أخرى مجموعة دائرية.

2. مجموعات فرعية من مجموعة دائرية لا حصر لها

.

3. مجموعات فرعية من المجموعة الدورية أعداد .

دليل.

دعونا نثبت 1 . يترك – مجموعة دورية تعسفية من النظام
. من أجل اليقين، سنفترض ذلك - المجموعة المضافة.

في هذه الحالة، العنصر المشترك للمجموعة يشبه

يترك
- مجموعة فرعية تعسفية غير تافهة من المجموعة ، أي.
.

لأن
ثم عناصر المجموعة الفرعية
هي عناصر النموذج
، لكن اذا.

من بين جميع عناصر النموذج
، حدد عنصرًا

، أين
– أصغر رقم موجب .

ثم أي
يمكن تمثيلها على النحو التالي:

من ماذا

لكن m هو أصغر رقم يحقق الشرط

ملغH  r = 0  H = ,

أولئك. H عبارة عن مجموعة حلقية تحتوي على عنصر التشكيل mg.

دعونا نثبت 2 . مجموعات فرعية من مجموعة دائرية لا حصر لها
يتم استنفادها من قبل مجموعات لا حصر لها
.

بالفعل منذ ذلك الحين
- المجموعة الدورية مع عنصر التوليد 1 أو
، أي.

إذن، وفقًا للفقرة 1 من هذه النظرية، أي مجموعة فرعية H من المجموعة الدائرية
يتم تحديده بواسطة عدد طبيعي
ويبدو

وكل هذه المجموعات الفرعية لا حصر لها.

دعونا نثبت 3 . مجموعات فرعية من المجموعة الدورية هي في المراسلات واحد لواحد مع المقسومات الإيجابية أعداد .

دعونا ، كما كان من قبل ،
- مجموعة ترتيبية دورية مضافة ، أي.

إذا، وإذا كان العنصر

نحن بحاجة إلى إثبات ذلك
يقسم .

في الواقع، دعونا نتخيل

ثم من حقيقة ذلك

,

والحد الأدنى
يتضمن
، لذلك
.

وهكذا من حقيقة ذلك
ويترتب على ذلك أن المجموعة الفرعية
لديه أمر ، أي.

.

متى
يمر عبر جميع المقسومات الإيجابية لعدد ، يفعل نفس الشيء ، وحصلنا على مجموعة فرعية واحدة بالضبط ، تقسيم .

عاقبة. في المجموعة الدورية
طلب مجموعة فرعية
طلب
يطابق العديد من العناصر
، مثل ذلك
.

دليل. عناصر المجموعة الدورية
طلب يبدو مثل

لو
، توي
.

العودة، واسمحوا
و
.

من الشرط
يتبع ذلك
، أين
و.

1. المقسومات العادية

لنفترض أن G تكون مجموعة عشوائية وH مجموعة فرعية من G، ثم إذا حصلنا على مجموعتين متبقيتين على اليسار
و
.

نريد معرفة الشروط التي يتم بموجبها ضرب العناصر المأخوذة من مجموعات التمام
و
، لا يعتمد على اختيار ممثلي الفئة وينتمي دائمًا إلى نفس فئة المجموعة مثل منتج العناصر
، أي الصف
.

عنصر ينتمي إلى فئة كوسيت
، والعنصر - الطبقة المجاورة
.

عناصر تعسفية تنتمي، على التوالي، إلى الطبقات المجاورة
و
يمكن تمثيلها على النحو التالي:

ثم منتجاتهم

يجب أن تنتمي إلى فئة

.

وهذا يعني أنه في المجموعة الفرعية H،

ضرب المساواة الناتجة على الحد الأيسر بحد ب ، لدينا:

(9)

أين

العلاقة (9) تسمح لنا بالتوصل إلى الاستنتاج التالي.

منذ العناصر
يتم اختيارها بشكل تعسفي، ثم لأي عنصر
وأي عنصر
هناك عنصر

,

العلاقة المرضية (9).

وبالإضافة إلى ذلك، العنصر
والعنصر
. ونتيجة لذلك، فإن كل مجموعة زاوية يسرى من المجموعة G بالنسبة إلى H تكون موجودة في مجموعة كاملة يمينية من المجموعة G بالنسبة إلى نفس المجموعة الفرعية H:

وبالمثل، يمكننا أن نظهر التضمين العكسي

وهذا سوف يعني ذلك

التعريف 1. تسمى المجموعة الفرعية H من المجموعة G المقسوم عليه عاديأو مجموعة فرعية ثابتة، إذا كان لأي مجموعتين g 1 H و g 2 H في المجموعة الفرعية H، المنتج
عناصر تعسفية
من هذه الفئات ينتمي إلى نفس فئة كوسيت
(الصورة 2).

أرز. 2– المجموعة الفرعية H هي مجموعة فرعية عادية من المجموعة G.

رسميًا: المجموعة الفرعية H – المقسوم عليه عاديمجموعات ، لو:

في المجموعات التبادلية، تكون كل مجموعة فرعية مقسومًا عاديًا (بسبب الطبيعة التبادلية لعملية الجمع).

للاستخدام العملي لمفهوم المقسوم عليه العادي، دعونا نفكر في بعض التعريفات "البناءة في التعامل".

التعريف 2. المجموعة الفرعية H من G هي المقسوم عليه عاديمن المجموعة G إذا وفقط إذا كانت كل مجموعة اليسار
يتزامن مع coset الصحيح
المجموعات G بواسطة H والعكس صحيح.

رسميًا: المجموعة الفرعية H – المقسوم عليه عاديالمجموعة ز إذا:

الشرط (12) يعني بوضوح أن:

أمثلة.

1. في أي مجموعة ز المجموعة نفسها
ووحدة المجموعة الفرعية
هي المقسومات العادية: مجموعات G اليسرى واليمنى حسب المجموعة الفرعية
يتكون من فئة واحدة مجاورة
، ومجموعات التمام اليسرى (اليمنى) للمجموعة الفرعية للوحدة H تتكون من جميع عناصر المجموعة G.

2. في كل مجموعة أبيلية G، كل مجموعة من مجموعاتها الفرعية H هي مجموعة فرعية عادية.

3. المجموعة المضاعفة للأعداد الحقيقية الموجبة
هو المقسوم عليه العادي للمجموعة المضاعفة لجميع الأعداد الحقيقية غير الصفر،

4. المجموعة المضاعفة للأعداد النسبية غير الصفرية
هو المقسوم عليه العادي للمجموعة المضاعفة للأعداد الحقيقية غير الصفرية

5. في مجموعة الضرب
المصفوفات غير المفردة
-المجموعة الفرعية من الترتيب ذات المعاملات الحقيقية
مصفوفات ذات محدد يساوي واحدًا:

هو المقسوم الطبيعي لهذه المجموعة.

في الواقع، مصفوفة الهوية
، لو

و

- على التوالي، المجموعتان اليسرى واليمنى للمجموعة
-المصفوفات غير المفردة
-الترتيب مع المعاملات الحقيقية على المجموعة الفرعية
- المصفوفات ذات المحدد يساوي واحد.

,

أولئك.
.

ومن ناحية أخرى، إذا

,

بسبب ال
لهذا

وبالتالي، من خلال تجميع جميع المصفوفات ذات المحددات المتساوية في مجموعة تامة واحدة (يسار أو يمين) نحصل على تحليل المجموعة
بواسطة مجموعة فرعية
. يوضح هذا المثال أن المجموعات غير التبادلية يمكن أن تحتوي أيضًا على مجموعات فرعية - المقسومات العادية، والتي لها مجموعة التمام اليسرى

يتزامن مع coset الصحيح

مجموعة فرعية حمجموعات زويسمى المقسوم العادي إذا كان لكل عنصر زمجموعات زمجموعاتها اليسرى واليمنى حسب المجموعة الفرعية حمتساوون، أي ز.ح=زئبق.

نظرية 2.5. مجموعة فرعية حمجموعات زهو المقسوم عليه عادي إذا وفقط إذا كان موجودا في حلأي زمن زو حمن ح.

دليلبوضوح.

يترك حهو المقسوم العادي للمجموعة ز. في مجموعة المجموعات، نقدم عملية الضرب الناتجة عن عملية المجموعة. تحت منتج الكوسيتات آهو البوسنة والهرسكسوف نفهم مجموعة جميع المنتجات الممكنة للعناصر من آهإلى العناصر البوسنة والهرسك. بسبب ال حهو المقسوم عليه بشكل طبيعي، فكل هذه المنتجات موجودة في فئة coset ( أب)ح. وهكذا، تم إدخال عملية على مجموعة من cosets. هذه العملية ترابطية ( أهبه)الفصل=آه(bHcH)، هناك عنصر محايد ح، ولكل عنصر آههناك عكس أ -1H. وبالتالي، فإن مجموعة مجموعات التمام بالنسبة للعملية المقدمة تشكل مجموعة تسمى مجموعة خارج القسمة.

تماثل المجموعات.

عرض جماعي فريد زإلى المجموعة ح، الذي يحافظ على العملية، يسمى التماثل الجماعي زالخامس ح.

التماثل هو حالة خاصة من التماثل.

الخاصية 2.9. في ظل التجانس، العنصر المحايد للمجموعة زيتم عرضه في عنصر المجموعة المحايدة ح.

دليليترتب على المساواة.

العديد من عناصر المجموعة ز، المعينة لعنصر محايد، تسمى نواة التماثل ويشار إليها بـ .

الخاصية 2.10.

دليل. منذ ذلك الحين.

الخاصية 2.11. نواة التجانس هو القاسم الطبيعي للمجموعة ز.

دليل. ل أمن زو بمن جوهر صحيح، وهذا هو.

العديد من عناصر المجموعة ح، وهي صور العناصر ز، ويسمى مجموعة من الصور ويدل على ذلك.

الخاصية 2.12. مجموعة الصور هي مجموعة فرعية ح.

دليلبوضوح.

نظرية 2.6. مجموعة العوامل متماثلة الشكل.

دليل. المراسلات هي واحد لواحد وتحافظ على العملية، ومن ثم فهي تحدد تماثل و.

نظرية 2.7. لأي مقسوم عادي حمجموعات زهناك تماثل نواته تساوي ح. على وجه الخصوص، مثل هذا التماثل من زالخامس ز/حيكون .

دليلبوضوح.

صف عادي

دعونا نثبت نظريتين حول التماثلات.

نظرية 2.8. يترك حمقسوم المجموعة العادي زو ص- مجموعة فرعية ز. ثم هو المقسوم عليه العادي صو

دليل. فليكن. ثم منذ ذلك الحين حالمقسوم عليه عادي ز، وبما أن جميع العناصر من ص. ولذلك، هو المقسوم العادي ص. المباراة هي واحد لواحد وتحافظ على العملية. لقد تم إثبات النظرية.

نظرية 2.9. يترك صهو المقسوم عليه العادي و . ثم ت- المقسوم العادي زو .

دليل. دعونا نفكر في مكان . منذ، ثم، و، يعني ت- المقسوم العادي ز. المراسلات هي من واحد إلى واحد، لأن ويحفظ العملية .

تسمى المجموعة بسيطة إذا لم يكن لها قاسم عادي غير نفسها ولا توجد مجموعة فرعية للوحدة.

السلسلة العادية للمجموعة هي سلسلة من المجموعات الفرعية التي تكون كل مجموعة لاحقة فيها مقسومًا عاديًا على المجموعة السابقة. إذا كانت جميع مجموعات السلسلة العادية موجودة في سلسلة عادية، فيقال إن السلسلة العادية الثانية تم الحصول عليها عن طريق تكثيف السلسلة العادية الأولى.

تسمى السلسلة العادية بدون تكرار والتي لا يمكن ضغطها بالتركيبية.

يتم تعريف العوامل لسلسلة عادية . تسمى سلسلتان عاديتان متماثلتان إذا كانت جميع عوامل السلسلة الأولى متشابهة مع عوامل السلسلة الثانية المعاد ترتيبها بترتيب معين.

الخاصية 2.13. إذا كانت السلسلة العادية متماثلة، فكل تكاثف من السلسلة الأولى يمكن العثور على تكاثف من السلسلة الثانية متماثلة لها.

دليل.لنفترض أن مجموعات فرعية جديدة ظهرت بين المجموعات الفرعية. بسبب ال وبالتالي، فإن العوامل متماثلة بالنسبة للمجموعات الفرعية المقابلة. دعونا نشير إلى المجموعة الفرعية المقابلة. دعونا نحدد تسلسل المجموعات، حيث أنا=1,…,ر. وفقا للنظرية المثبتة أعلاه. وبالتالي، فإن ضغط الصف الثاني بواسطة المجموعات يكون متماثلًا. وقد ثبت الملكية.