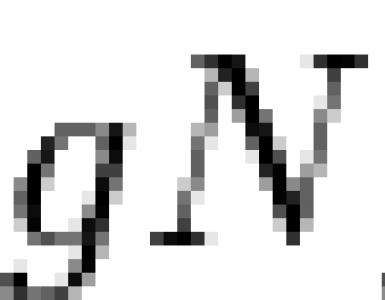சாதாரண குழு வகுப்பான். சாதாரண குழு வகுப்பிகள் சாதாரண குழு வகுப்பாளர்

தொடர்புடைய வகுப்புகள். ஒரு குழுவை ஒரு துணைக்குழுவாக சிதைப்பது

ஒரு குழுவாக இருக்கட்டும், அதன் துணைக்குழுவாக இருக்கட்டும், குழுவின் தன்னிச்சையான அங்கமாக இருக்கட்டும். ஒரு செட் செய்வோம். இந்த வெறுமையற்ற தொகுப்பு அழைக்கப்படுகிறது இடது கோசெட்உறுப்பு மூலம் வரையறுக்கப்பட்ட துணைக்குழு மூலம் குழுக்கள். தொகுப்பு அழைக்கப்படுகிறது சரியான கோசெட்உறுப்பு மூலம் வரையறுக்கப்பட்ட துணைக்குழு மூலம் குழுக்கள். பொதுவாக .

சிக்கல் 61. B துணைக்குழுவாக இருந்தால் உறுப்பு மூலம் வரையறுக்கப்பட்ட வலது மற்றும் இடது இணைத்தொகுப்புகளைக் கண்டறியவும்.

தீர்வு.

வகுப்புகளை உருவாக்குவோம்

குறிப்பு, .

ஒரு குழுவாகவும் அதன் துணைக்குழுவாகவும் இருக்கட்டும்.

என்றால், துணைக்குழுவின் குழு ஒரு கோசெட்டாக சிதைகிறது என்று அவர்கள் கூறுகிறார்கள்.

ஒரு உறுப்பு இருந்தால், நாங்கள் ஒரு வகுப்பை உருவாக்குவோம்.

எனில், குழுவானது துணைக்குழுவால் இரண்டு இடது கோசெட்களாக சிதைக்கப்படும்.

என்றால், துணைக்குழுவைப் பொறுத்தமட்டில், குழுவை மூன்று கூட்டுத்தொகுப்புகளாகப் பிரித்துள்ளோம்.

ஒரு குழுவை ஒரு துணைக்குழுவாக இடது கோசெட்களாக சிதைக்கும் செயல்முறை வரையறுக்கப்பட்டதாகவோ அல்லது எல்லையற்றதாகவோ இருக்கலாம்.

இதேபோல், துணைக்குழுவின் மூலம் ஒரு குழுவின் சிதைவை சரியான கோசெட்களாகப் பெறலாம்: .

வலது சிதைவு இடது சிதைவுடன் ஒத்துப்போக வேண்டியதில்லை.

இதன் விளைவாக, நாங்கள் இரண்டு செட் வகுப்புகளைப் பெறுகிறோம்:

மற்றும் துணைக்குழுவின் அடிப்படையில் இடது மற்றும் வலது காரணி தொகுப்புகள். இந்த தொகுப்புகளின் நீளம் அழைக்கப்படுகிறது குறியீட்டுஒரு குழுவில் துணைக்குழுக்கள்.

சிக்கல் 62.கூட்டல் செயல்பாட்டைப் பொறுத்து துணைக்குழுவின் மூலம் ஒரு தொகுப்பின் காரணி தொகுப்பைக் கண்டறியவும்.

தீர்வு.கூட்டல் செயல்பாடு மாற்றத்தக்கது, எனவே இடது மற்றும் வலது விரிவாக்கங்கள் ஒரே மாதிரியாக இருக்கும். இடது கோசெட்களாக சிதைவோம்.

உதாரணத்திற்கு, . நாங்கள் கட்டுகிறோம். . நாம் இரண்டு அடுத்தடுத்த வகுப்புகளாக ஒரு சிதைவைக் கொண்டுள்ளோம். காரணி தொகுப்பு: .

சிக்கல் 63.பெருக்கல் குழுவில்

ஒரு துணைக்குழுவை எடுத்துக் கொள்வோம். மூலம் ஒரு தொகுப்பின் காரணி தொகுப்பைக் கண்டறியவும்.

தீர்வு.இடது கை விரிவாக்கத்துடன் எங்களிடம் உள்ளது:

அதாவது, ஒரு இடது பக்க காரணி தொகுப்பு.

வலது கை விரிவாக்கத்துடன் எங்களிடம் உள்ளது:

அதாவது, ஒரு வலது பக்க காரணி தொகுப்பு , மற்றும் , .

துணைக்குழுக் குறியீடு 3 ஆகும்.

சிக்கல் 64. 3 இன் பெருக்கல் முழு எண்களின் துணைக்குழுவில் சேர்க்கை குழுவின் சிதைவைக் கண்டறியவும்.

தீர்வு. .

உதாரணத்திற்கு, . அதை உருவாக்குவோம். எனவே, வர்க்கமானது 3 ஆல் வகுக்கும் போது 1 இன் மீதியை விட்டுவிடும் அனைத்து முழு எண்களையும் கொண்டுள்ளது. எடுத்துக்காட்டாக, , . அதை உருவாக்குவோம். இதன் விளைவாக, வர்க்கம் அனைத்து முழு எண்களைக் கொண்டுள்ளது, அவை 3 ஆல் வகுக்கும் போது, ​​​​2 இன் மீதியை விட்டு விடுங்கள். எனவே, 3 ஆல் வகுத்தால், 0 இன் மீதியை விட்டு, வகுப்பில் வகுக்கப்படும் அனைத்து முழு எண்களும் உள்ளன. 3 ஆல், மீதி 1 இல், வகுப்பில் - மீதமுள்ள 2 உடன் அனைத்து எண்களும். ஆனால் 3 ஆல் வகுத்தால், மீதமுள்ள 0, 1, 2 மட்டுமே சாத்தியமாகும். இதன் பொருள் அனைத்து முழு எண்களும் வகுப்புகள் முழுவதும் விநியோகிக்கப்படுகின்றன, அதாவது, அருகிலுள்ள வகுப்புகளாக சிதைவு மூலம் வடிவம் உள்ளது: . கூட்டல் பரிமாற்றமானது என்பதால், இடது கை விரிவாக்கம் வலது கை விரிவாக்கத்துடன் ஒத்துப்போகிறது. துணைக்குழுக் குறியீடு 3 ஆகும்.

சாதாரண குழு வகுப்பான். காரணி குழு

ஒரு குழு எந்த உறுப்புக்கும் தொடர்புடைய துணைக்குழுவைக் கொண்டிருந்தால், அதாவது, குழுவின் எந்த உறுப்பும் துணைக்குழுவுடன் பயணித்தால், அந்த துணைக்குழு குழுவின் சாதாரண வகுப்பான் என்று அழைக்கப்படுகிறது.

ஒரு குழுவில் ஒரு செயல்பாடு பரிமாற்றமாக இருந்தால், குழுவில் உள்ள எந்த துணைக்குழுவும் ஒரு சாதாரண வகுப்பான். ஒரு குழுவின் இடது பக்க மற்றும் வலது பக்க சிதைவுடன் ஒரு துணைக்குழுவாக இருந்தால், குழுவின் சிதைவுகள் ஒரே மாதிரியாக மாறினால், குழுவின் ஒரு சாதாரண வகுப்பான். உரையாடலும் உண்மைதான்: குழுவில் ஒரு சாதாரண வகுப்பியாக இருந்தால், குழுவின் இடது பக்க மற்றும் வலது பக்கச் சிதைவுடன் ஒரு துணைக்குழுவாக, குழு சிதையும் கோசெட்கள் ஒரே மாதிரியாக மாறும்.

ஒரு குழுவின் இயல்பான வகுத்தல், ஏதேனும் ஒரு உறுப்பு இருந்தால் மட்டுமே.

சிக்கல் 65.ஒரு குழுவின் துணைக்குழு குறியீடு 2 எனில், குழுவின் சாதாரண வகுப்பான்.

தீர்வு.ஒரு துணைக்குழுவில் குழுவில் குறியீட்டு 2 இருந்தால் , எங்கே மற்றும் , அதாவது . இதன் விளைவாக, இடது பக்க சிதைவின் கூட்டுத்தொகைகள் வலது பக்க சிதைவின் தொடர்புடைய வகுப்புகளுடன் ஒத்துப்போகின்றன, அதாவது குழுவின் ஒரு சாதாரண வகுப்பான்.

சிக்கல் 66.சிக்கல் 63 இல் உள்ள குழு குழுவில் ஒரு சாதாரண வகுப்பாளராக இருக்குமா?

தீர்வு.துணைக்குழுவாக ஒரு குழுவின் இடது பக்க சிதைவு வகுப்புகள் மற்றும் . வலது கை சிதைவு வகுப்புகளைக் கொண்டுள்ளது , , , ஆனால் , , அதாவது, துணைக்குழு குழுவின் சாதாரண வகுப்பான் அல்ல.

சிக்கல் 67. 3 இன் பெருக்கல் அனைத்து எண்களின் துணைக்குழுவில் கொடுக்கப்பட்ட குழுவின் காரணி குழுவைக் கண்டறியவும்.

தீர்வு.உள்ள கூட்டல் பரிமாற்றம் என்பதால், இது ஒரு சாதாரண வகுப்பி. இதில் விரிவாக்கத்தைக் கண்டறிவோம்: . ஒரு காரணி தொகுப்பு வகுப்புகளைக் கொண்டுள்ளது. கூட்டல் செயல்பாட்டை அமைப்போம்:

கேலி அட்டவணையை நிரப்புவது விதியின் படி மேற்கொள்ளப்படுகிறது:

உதாரணத்திற்கு, . இந்த தொகுப்பு அனைத்து முழு எண்களையும் கொண்டுள்ளது, அதாவது, . பிறகு . எனவே, நாங்கள் ஒரு காரணிக் குழுவைப் பெற்றுள்ளோம், இதில் மேலே குறிப்பிடப்பட்ட கேலி அட்டவணையில் சேர்க்கப்படும் செயல்பாடு வழங்கப்படுகிறது.

சிக்கல் 68.துணைக்குழு மூலம் ஒரு குழுவின் காரணிக் குழுவைக் கண்டறியவும்.

தீர்வு.ஒரு சாதாரண வகுப்பான், ஏனெனில் உள்ள கூட்டல் மாற்றத்திற்குரியது. இதில் விரிவாக்கத்தைக் கண்டறிவோம்: . உண்மையில், அதை எண் அச்சில் சித்தரிப்போம், அதில் உள்ள உறுப்புகளை புள்ளிகளால் குறிக்கவும்:

எங்கே கட்டலாம். என்றால் , பின்னர் , என்றால் , பின்னர் உறுப்புகளை நட்சத்திரக் குறியீடுகளால் குறிக்கிறோம். பின்னர் புள்ளிகள் மற்றும் நட்சத்திரங்களுடன் குறிக்கப்பட்ட கூறுகளைக் கொண்டுள்ளது. இந்த தொகுப்பில் ஒரு உறுப்பு இல்லை, எடுத்துக்காட்டாக, . பின்னர் நாம் ஒரு தொகுப்பை உருவாக்குகிறோம், அதன் கூறுகளை ஒரு பிரைம் மூலம் குறிக்கிறோம். பின்னர் அது புள்ளிகள், நட்சத்திரங்கள் மற்றும் ப்ரைம்களால் குறிக்கப்பட்ட கூறுகளைக் கொண்டுள்ளது, ஆனால் உடன் ஒத்துப்போவதில்லை. வெளிப்படையாக, உடன் ஒத்துப்போவதற்கு, அது அவசியம்.

நாங்கள் ஒரு காரணி தொகுப்பை உருவாக்கியுள்ளோம். காரணிமயமாக்கல் நடைமுறையின் படி, கூட்டல் செயல்பாடு பின்வருமாறு வரையறுக்கப்படுகிறது: , எங்கே , .

அறிமுகம் 2
1. குழுக்களின் வரையறை மற்றும் எடுத்துக்காட்டுகள் 4
2. துணைக்குழுக்கள் 8
3. சுழற்சி குழுக்கள். 13
4. இயல்பான வகுப்பிகள், காரணி குழுக்கள் 17
5. ஒரு குழுவிற்குள் ஒரு துணைக்குழுவின் இலட்சியம். லாக்ரேங்கின் தேற்றம் மற்றும் அதன் விளைவுகள். 22
6. சிக்கல்களைத் தீர்க்கும் போது குழுக்களின் சாதாரண வகுப்பிகளைப் பயன்படுத்துதல் 26
முடிவு 29
குறிப்புகள் 30

அறிமுகம்

உயர் இயற்கணிதம் ஒரு தொலைநோக்கு, ஆனால் ஆரம்ப இயற்கணிதத்தின் பள்ளி பாடத்தின் முக்கிய உள்ளடக்கத்தின் இயல்பான பொதுமைப்படுத்தல் ஆகும். லீனியர் இயற்கணிதம், இது முக்கியமாக மெட்ரிக் கோட்பாடு மற்றும் திசையன் இடங்களின் நேரியல் மாற்றங்களின் கோட்பாட்டிற்கு அர்ப்பணிக்கப்பட்ட ஒரு பெரிய அறிவியலாகும், இது வடிவங்களின் கோட்பாடு, மாறுபாடுகளின் கோட்பாடு மற்றும் டென்சர் இயற்கணிதம் ஆகியவற்றை உள்ளடக்கியது, இது வேறுபட்ட வடிவவியலில் முக்கிய பங்கு வகிக்கிறது. திசையன் இடைவெளிகளின் கோட்பாடு இயற்கணிதத்திற்கு வெளியே, செயல்பாட்டு பகுப்பாய்வில் (எல்லையற்ற பரிமாண இடைவெளிகள்) மேலும் உருவாக்கப்பட்டுள்ளது. கணிதம் மற்றும் இயக்கவியல், இயற்பியல் மற்றும் தொழில்நுட்ப அறிவியல் ஆகிய இரண்டிலும் அதன் பயன்பாடுகளின் பல்வேறு மற்றும் முக்கியத்துவத்தின் அடிப்படையில், இயற்கணிதத்தின் பல கிளைகளில் நேரியல் இயற்கணிதம் முதன்மையானது.
புலக் கோட்பாடு சமன்பாடுகளின் கோட்பாட்டின் மேலும் வளர்ச்சிக்கான இயற்கையான பகுதியாக மாறியது, மேலும் அதன் முக்கிய கிளைகள் - இயற்கணித எண் புலங்களின் கோட்பாடு மற்றும் இயற்கணித செயல்பாட்டு புலங்களின் கோட்பாடு - முறையே எண் கோட்பாடு மற்றும் செயல்பாடுகளின் கோட்பாட்டுடன் இணைக்கப்பட்டது. ஒரு சிக்கலான மாறியின். உயர் இயற்கணிதம் பாடமானது புலக் கோட்பாட்டிற்கான ஆரம்ப அறிமுகத்தை உள்ளடக்கியது, மேலும் பாடத்தின் சில பிரிவுகள் - பல தெரியாதவற்றில் உள்ள பல்லுறுப்புக்கோவைகள், மேட்ரிக்ஸின் இயல்பான வடிவம் - ஒரு தன்னிச்சையான அடிப்படை புலத்திற்கு உடனடியாக வழங்கப்படுகின்றன.
ஒரு புலத்தின் கருத்தை விட பரந்த கருத்து ஒரு வளையம். ஒரு புலத்தைப் போலல்லாமல், இங்கு வகுப்பதற்கான சாத்தியக்கூறுகள் தேவைப்படாது, மேலும், பெருக்கல் என்பது பரிமாற்றம் அல்லாதது மற்றும் தொடர்புடையது அல்ல. மோதிரங்களின் எளிய எடுத்துக்காட்டுகள் அனைத்து முழு எண்களின் தொகுப்பு (எதிர்மறையானவை உட்பட), தெரியாத ஒன்றில் பல்லுறுப்புக்கோவைகளின் அமைப்பு மற்றும் உண்மையான மாறியின் உண்மையான செயல்பாடுகளின் அமைப்பு. ரிங் கோட்பாட்டில் ஹைபர்காம்ப்ளக்ஸ் அமைப்புகளின் கோட்பாடு மற்றும் இலட்சியங்களின் கோட்பாடு போன்ற இயற்கணிதத்தின் பழைய கிளைகள் அடங்கும், இது பல கணித அறிவியலுடன் / குறிப்பாக செயல்பாட்டு பகுப்பாய்வுடன் தொடர்புடையது மற்றும் ஏற்கனவே இயற்பியலில் சில விற்பனை நிலையங்களைக் கண்டறிந்துள்ளது. உயர் இயற்கணிதத்தின் போக்கில், சாராம்சத்தில், ஒரு வளையத்தின் கருத்தின் வரையறை மட்டுமே உள்ளது.
குழுக் கோட்பாடு இன்னும் பெரிய அளவிலான பயன்பாடுகளைக் கொண்டுள்ளது. ஒரு குழு என்பது ஒரு அடிப்படைச் செயல்பாட்டைக் கொண்ட ஒரு இயற்கணித அமைப்பாகும், மேலும் இந்தச் செயல்பாடு துணையாக இருக்க வேண்டும், இருப்பினும் பரிமாற்றம் அவசியமில்லை, மேலும் ஒரு தலைகீழ் செயல்பாட்டைக் கொண்டிருக்க வேண்டும் - பிரிவு, முக்கிய செயல்பாடு பெருக்கல் என்று அழைக்கப்பட்டால். எடுத்துக்காட்டாக, கூட்டல் செயல்பாட்டைப் பொறுத்து கருதப்படும் முழு எண்களின் தொகுப்பு, அத்துடன் பெருக்கத்தின் செயல்பாட்டுடன் கருதப்படும் நேர்மறை உண்மையான எண்களின் சேகரிப்பு. குழுக்கள் ஏற்கனவே கலோயிஸ் கோட்பாட்டில், தீவிர சமன்பாடுகளின் தீர்வு பற்றிய கேள்வியில் ஒரு பெரிய பங்கைக் கொண்டிருந்தன, ஆனால் இப்போது அவை புலக் கோட்பாட்டிலும், வடிவவியலின் பல கிளைகளிலும், இடவியலிலும், கணிதத்திற்கு வெளியேயும் - படிகவியலில் ஒரு முக்கிய கருவியாக உள்ளன. கோட்பாட்டு இயற்பியலில். பொதுவாக, அதன் பயன்பாட்டுத் துறையின் அகலத்தைப் பொறுத்தவரை, குழுக் கோட்பாடு இயற்கணிதத்தின் அனைத்து கிளைகளிலும் நேரியல் இயற்கணிதத்திற்கு அடுத்ததாக உள்ளது.
இந்த வேலையின் பொருள் குழுக்களின் சாதாரண வகுப்பிகள்.
பணிகள்:
1. ஒரு குழு மற்றும் துணைக்குழுவை வரையறுத்து, குழுக்களின் உதாரணங்களைக் கவனியுங்கள்.
2. சுழற்சிக் குழுக்களைக் கவனியுங்கள்.
3. சாதாரண வகுப்பிகளின் கருத்தைக் கவனியுங்கள்
4. லாக்ரேங்கின் தேற்றத்தையும் அதிலிருந்து விளைவுகளையும் கொடுங்கள்.
5. சிக்கல்களைத் தீர்க்கும் போது சாதாரண குழு வகுப்பிகளைப் பயன்படுத்துவதைக் கவனியுங்கள்.

பயன்படுத்தப்பட்ட ஆதாரங்களின் பட்டியல்

1. குலிகோவ் எல்.யா. மற்றும் எண் கோட்பாடு: பாடநூல். கல்வி நிறுவனங்களுக்கான கையேடு. – : அதிக பள்ளி, 1979. - 559 ப., நோய்.
2. கோஸ்ட்ரிகின் ஏ.ஐ. அல்ஜீப்ரா அறிமுகம்: பல்கலைக்கழகங்களுக்கான பாடநூல். – எம்.: ஃபிஸ்மாட்லிட், 2004. – 272 பக்.
3. ஃபதேவ் டி.கே. உயர் இயற்கணிதத்தில் உள்ள சிக்கல்களின் தொகுப்பு. – எம்.: நௌகா, 1977. – 288 பக்.
4. குரோஷ் ஏ.ஜி. உயர் அல்ஜீப்ரா படிப்பு. – எம்.: நௌகா, 1968.
5. ஒகுனேவ் எல்.யா. உயர் இயற்கணிதத்தில் உள்ள சிக்கல்களின் தொகுப்பு - எம்.: கல்வி, 1964.

மொத்த அளவு: 30 பக்.

ஆண்டு: 2013

வரையறைகள்

துணைக்குழு என்குழுக்கள் ஜிஅழைக்கப்பட்டது சாதாரண, இது இணைவுகளின் கீழ் மாறாததாக இருந்தால், அதாவது, எந்த உறுப்புக்கும் nஇருந்து என்மற்றும் ஏதேனும் gஇருந்து ஜி, உறுப்பு gng − 1 உள்ளது என் :

பின்வரும் துணைக்குழு இயல்பான நிலைமைகள் சமமானவை:

நிபந்தனை (1) தர்க்கரீதியாக (2) விட பலவீனமானது, மற்றும் நிபந்தனை (3) தர்க்கரீதியாக (4) விட பலவீனமானது. எனவே, துணைக்குழுவின் இயல்பான தன்மையை நிரூபிக்கும் போது நிபந்தனைகள் (1) மற்றும் (3) அடிக்கடி பயன்படுத்தப்படுகின்றன, மேலும் நிபந்தனைகள் (2) மற்றும் (4) இயல்புநிலையின் விளைவுகளை நிரூபிக்க பயன்படுத்தப்படுகின்றன.

எடுத்துக்காட்டுகள்

• {இ) மற்றும் ஜி- எப்போதும் சாதாரண துணைக்குழுக்கள் ஜி. அவை அற்பமானவை என்று அழைக்கப்படுகின்றன. வேறு சாதாரண துணைக்குழுக்கள் இல்லை என்றால், குழு ஜிஎளிமையானது என்று அழைக்கப்படுகிறது.

• குழுவின் மையம் ஒரு சாதாரண துணைக்குழுவாகும்.

• ஒரு குழுவின் கம்யூட்டர் ஒரு சாதாரண துணைக்குழு.

• எந்தவொரு குணாதிசயமான துணைக்குழுவும் இயல்பானது, ஏனெனில் இணைதல் எப்போதும் ஒரு தன்னியக்கமாகும்.

• அனைத்து துணைக்குழுக்கள் என்அபிலியன் குழு ஜிசாதாரணமாக இருப்பதால் gஎன் = என்g . ஒவ்வொரு துணைக்குழுவும் இயல்பானதாக இருக்கும் அபிலியன் அல்லாத குழு ஹாமில்டோனியன் என்று அழைக்கப்படுகிறது.

• எந்தவொரு பரிமாணத்தின் இடைவெளியிலும் இணையான மொழிபெயர்ப்புகளின் குழு யூக்ளிடியன் குழுவின் சாதாரண துணைக்குழுவாகும்; எடுத்துக்காட்டாக, முப்பரிமாண இடத்தில், சுழற்சி, மொழிபெயர்ப்பு மற்றும் எதிர் திசையில் சுழற்சி ஒரு எளிய மொழிபெயர்ப்புக்கு வழிவகுக்கிறது.

• ரூபிக்ஸ் கியூப் குழுவில், மூலை உறுப்புகளில் மட்டுமே செயல்படும் செயல்பாடுகளைக் கொண்ட ஒரு துணைக்குழு இயல்பானது, ஏனெனில் எந்த ஒரு கூட்டு உருமாற்றமும் அத்தகைய செயல்பாட்டை ஒரு மூலை உறுப்புக்கு பதிலாக விளிம்பு உறுப்பு மீது செயல்பட வைக்காது. இதற்கு நேர்மாறாக, மேல் முகத்தின் சுழற்சிகளை மட்டுமே கொண்ட துணைக்குழு சாதாரணமானது அல்ல, ஏனெனில் துணைவர்கள் மேல் முகத்தின் பகுதிகளை கீழே நகர்த்த அனுமதிக்கின்றனர்.

பண்புகள்

• இயல்புநிலையானது surjective homomorphisms மற்றும் தலைகீழ் படங்களை எடுப்பதன் கீழ் பாதுகாக்கப்படுகிறது.
• ஒரு நேரடி தயாரிப்பை உருவாக்கும்போது இயல்புநிலை பாதுகாக்கப்படுகிறது.
• ஒரு சாதாரண துணைக்குழுவின் சாதாரண துணைக்குழு குழுவில் சாதாரணமாக இருக்க வேண்டிய அவசியமில்லை, அதாவது இயல்புநிலை மாறாது. இருப்பினும், ஒரு சாதாரண துணைக்குழுவின் சிறப்பியல்பு துணைக்குழு இயல்பானது.
• குறியீட்டு 2 இன் ஒவ்வொரு துணைக்குழுவும் இயல்பானது. என்றால் ப- சிறிய முதன்மை வரிசை வகுப்பான் ஜி, பின்னர் குறியீட்டின் ஏதேனும் துணைக்குழு பசாதாரண.
• என்றால் என்- சாதாரண துணைக்குழு ஜி, பின்னர் இடது (வலது) கோசெட்களின் தொகுப்பில் ஜி / என்நீங்கள் விதியின் படி குழு கட்டமைப்பை உள்ளிடலாம்

(g 1 என்)(g 2 என்) = (g 1 g 2)என் இதன் விளைவாக வரும் தொகுப்பு காரணி குழு என்று அழைக்கப்படுகிறது ஜிமூலம் என் .

• என்இடது கோசெட்களில் அற்பமாக செயல்பட்டால் மட்டுமே இயல்பானது ஜி / என் .

வரலாற்று உண்மைகள்

சாதாரண துணைக்குழுக்களின் முக்கியத்துவத்தை முதலில் புரிந்துகொண்டவர் Évariste Galois.

இணைப்புகள்

• வின்பெர்க் ஈ. பி.அல்ஜீப்ரா பாடநெறி - எம்.: ஃபேக்டோரியல் பிரஸ் பப்ளிஷிங் ஹவுஸ், 2002, ISBN 5-88688-060-7

விக்கிமீடியா அறக்கட்டளை. 2010.

• சாதாரண மார்கோவ் அல்காரிதம்
• சாதாரண மின்முனை திறன்

மற்ற அகராதிகளில் "இயல்பான வகுத்தல்" என்றால் என்ன என்பதைப் பார்க்கவும்:

சாதாரண வகுப்பான்- மாறாத துணைக்குழு, குழுக் கோட்பாட்டின் அடிப்படைக் கருத்துக்களில் ஒன்று (குழுவைப் பார்க்கவும்), இ. கலோயிஸ் அறிமுகப்படுத்தினார். G குழுவின் N. d கிரேட் சோவியத் என்சைக்ளோபீடியா

சாதாரண பிரிவு- ஒரு சாதாரண துணைக்குழு, மாறாத துணைக்குழு, G இன் துணைக்குழு H, இதற்கு துணைக்குழு H இல் உள்ள G குழுவின் இடது பக்க சிதைவு வலது பக்கத்துடன் ஒத்துப்போகிறது, அதாவது, எந்த உறுப்புக்கும் ஒரு துணைக்குழு aH மற்றும் Ha ஆகியவை சமம் (பொருளில்... ... கணித கலைக்களஞ்சியம்

துணைக்குழுக்களின் இயல்பான தொடர்- குழுக் கோட்பாட்டின் பொதுவான விளக்கத்திற்கு, குழு (கணிதம்) மற்றும் குழுக் கோட்பாட்டைப் பார்க்கவும். சாய்வு இந்த அகராதியின் குறிப்பைக் குறிக்கிறது. # ஏ பி சி டி இ ஈ எஃப் ஜி எச் ஐ ஜே ஜே கே எல் எம் என் ஓ பி ஆர் எஸ் டி யு ... விக்கிபீடியா

சாதாரண வரிசை- குழுக் கோட்பாட்டின் பொதுவான விளக்கத்திற்கு, குழு (கணிதம்) மற்றும் குழுக் கோட்பாட்டைப் பார்க்கவும். சாய்வு இந்த அகராதியின் குறிப்பைக் குறிக்கிறது. # A B C D E E F G H I J J K L M N O P R S T U ... விக்கிபீடியா ஒரு இடவியல் குழு, இடவியல் குழுவாக கச்சிதமானது. விண்வெளி. எடுத்துக்காட்டாக, ஒவ்வொரு வரையறுக்கப்பட்ட குழுவும் (தனிப்பட்ட இடவியலில்) ஒரு இயற்கணிதக் குழுவாகும், இருப்பினும் இது ஒரு சிறிய இடவியல் குழுவாகும். விண்வெளி (ஜாரிஸ்கி இடவியல் தொடர்பானது) ... கணித கலைக்களஞ்சியம்

லீ - கொல்சினா தேற்றம்- GL(V) குழுவின் தீர்க்கக்கூடிய துணைக்குழு G (V என்பது இயற்கணித ரீதியாக மூடிய புலத்தின் மீது வரையறுக்கப்பட்ட பரிமாண திசையன் இடைவெளி) குறியீட்டின் ஒரு சாதாரண வகுப்பான் G1 ஐக் கொண்டுள்ளது, அங்கு p மங்கலான V ஐ மட்டுமே சார்ந்துள்ளது, அதாவது V இல் உள்ளது G1 ஐப் பொறுத்தமட்டில் ஒரு கொடி மாறாதது.… கணித கலைக்களஞ்சியம்

இடவியல் குழு- ஒரு தொகுப்பு G, இதில் இரண்டு குழு கட்டமைப்புகள் மற்றும் ஒரு இடவியல் அமைப்பு கொடுக்கப்பட்டுள்ளது. குழு செயல்பாடுகளின் தொடர்ச்சியின் நிபந்தனைக்கு இசைவான இடைவெளிகள். அதாவது, ஒரு நேரடி தயாரிப்பை G இல் மேப்பிங் செய்வது தொடர்ச்சியாக இருக்க வேண்டும். துணைக்குழு N T. g. G என்பது T. g. in... ... கணித கலைக்களஞ்சியம்

Lagrange இன் தேற்றம் கூறுகிறது என்றால் , a
, அந்த

அந்த. உத்தரவு
G குழுவின் எந்த துணைக்குழு H ஐயும் G குழுவின் வரிசையாக N பிரிக்கிறது.

இயற்கையாகவே, தேற்றத்தின் தலைகீழ் பற்றி கேள்வி எழுகிறது: m என்றால் ஒரு வகுப்பான்
, பின்னர் G வரிசை m இன் துணைக்குழு H உள்ளதா?

வேறு வார்த்தைகளில் கூறுவதானால்: குழு N இன் வரிசையின் ஒவ்வொரு வகுப்பி m க்கும், m வரிசையின் G குழுவின் H துணைக்குழு உள்ளதா?

பொதுவாக, பதில் எதிர்மறையானது, ஆனால் சில சிறப்பு சந்தர்ப்பங்களில் இது மேல்முறையீடுலாக்ரேங்கின் தேற்றம் உண்மை.

தேற்றம். (லாக்ரேஞ்ச் தேற்றத்தின் தலைகீழ் )

1. சுழற்சிக் குழுவின் ஒவ்வொரு துணைக்குழுவும் மீண்டும் ஒரு சுழற்சிக் குழுவாகும்.

2. எல்லையற்ற சுழற்சிக் குழுவின் துணைக்குழுக்கள்

.

3. வரிசையின் சுழற்சிக் குழுவின் துணைக்குழுக்கள் எண்கள் .

ஆதாரம்.

நிரூபிப்போம் 1 . விடுங்கள் - ஒழுங்கின் தன்னிச்சையான சுழற்சி குழு
. திட்டவட்டமாக, நாங்கள் அதைக் கருதுவோம் - சேர்க்கை குழு.

இந்த வழக்கில், குழுவின் பொதுவான உறுப்பு போல் தெரிகிறது

விடுங்கள்
- குழுவின் தன்னிச்சையான அல்லாத அற்பமான துணைக்குழு , அதாவது
.

ஏனெனில்
, பின்னர் துணைக்குழுவின் கூறுகள்
வடிவத்தின் கூறுகளாகும்
, ஆனால் என்றால்.

வடிவத்தின் அனைத்து கூறுகளிலும்
, ஒரு உறுப்பைத் தேர்ந்தெடுக்கவும்

, எங்கே
- மிகச்சிறிய நேர்மறை எண்.

பின்னர் ஏதேனும்
இவ்வாறு குறிப்பிடலாம்:

எதிலிருந்து

ஆனால் m என்பது நிபந்தனையை பூர்த்தி செய்யும் மிகச்சிறிய எண்

mgH  r = 0  H = ,

அந்த. H என்பது ஒரு சுழற்சிக் குழுவாக உருவாகும் உறுப்பு mg.

நிரூபிப்போம் 2 . எல்லையற்ற சுழற்சிக் குழுவின் துணைக்குழுக்கள்
எல்லையற்ற குழுக்களால் தீர்ந்துவிட்டது
.

உண்மையில், இருந்து
- உறுப்பு 1 ஐ உருவாக்கும் சுழற்சி குழு அல்லது
, அதாவது

பின்னர், இந்த தேற்றத்தின் பத்தி 1 இன் படி, சுழற்சி குழுவின் எந்த துணைக்குழு H
இயற்கை எண்ணால் தீர்மானிக்கப்படுகிறது
மற்றும் போல் தெரிகிறது

இந்த துணைக்குழுக்கள் அனைத்தும் எல்லையற்றவை.

நிரூபிப்போம் 3 . வரிசையின் சுழற்சிக் குழுவின் துணைக்குழுக்கள் நேர்மறை வகுப்பிகளுடன் ஒன்றுக்கு ஒன்று கடிதப் பரிமாற்றத்தில் உள்ளன எண்கள் .

முன்பு போல், விடுங்கள்
- வரிசையின் சேர்க்கை சுழற்சி குழு , அதாவது

என்றால், மற்றும் உறுப்பு என்றால்

என்பதை நாம் நிரூபிக்க வேண்டும்
பிரிக்கிறது .

உண்மையில், கற்பனை செய்வோம்

பின்னர் உண்மையில் இருந்து

,

மற்றும் குறைந்தபட்சம்
ஏற்படுத்துகிறது
, எனவே
.

இவ்வாறு, உண்மையில் இருந்து
, அது துணைக்குழு என்று பின்வருமாறு
ஒழுங்கு உள்ளது , அதாவது

.

எப்பொழுது
ஒரு எண்ணின் அனைத்து நேர்மறை வகுப்பிகளிலும் இயங்குகிறது , அதையே செய்கிறது , மற்றும் வரிசையின் ஒரு துணைக்குழுவைப் பெறுகிறோம் , பிரித்தல் .

விளைவு. சுழற்சி குழுவில்
உத்தரவு துணைக்குழு
உத்தரவு
பல கூறுகளுடன் பொருந்துகிறது
, அதுபோல்
.

ஆதாரம். சுழற்சி குழுவின் கூறுகள்
உத்தரவு போல் இருக்கும்

என்றால்
, தோய்
.

மீண்டும், விடு
மற்றும்
.

நிலையில் இருந்து
அதை பின்பற்றுகிறது
, எங்கே
மற்றும்.

1. சாதாரண வகுப்பிகள்

G ஒரு தன்னிச்சையான குழுவாகவும், H என்பது G இன் துணைக்குழுவாகவும் இருக்கட்டும், அப்படியானால் நாம் இரண்டு இடது கோசெட்களைப் பெறுவோம்.
மற்றும்
.

கோசெட்களில் இருந்து எடுக்கப்பட்ட தனிமங்களின் தயாரிப்பு எந்த நிலையில் உள்ளது என்பதை அறிய விரும்புகிறோம்
மற்றும்
, வர்க்கப் பிரதிநிதிகளின் தேர்வைச் சார்ந்து இல்லை மற்றும் எப்போதும் தனிமங்களின் உற்பத்தியின் அதே கோசெட் வகுப்பைச் சேர்ந்தது
, அதாவது வகுப்பு
.

உறுப்பு கோசெட் வகுப்பைச் சேர்ந்தது
, மற்றும் உறுப்பு - அருகில் உள்ள வகுப்பு
.

தன்னிச்சையான கூறுகள் முறையே, அருகிலுள்ள வகுப்புகளுக்குச் சொந்தமானது
மற்றும்
இவ்வாறு குறிப்பிடலாம்:

பின்னர் அவர்களின் தயாரிப்பு

ஒரு வகுப்பைச் சேர்ந்தவராக இருக்க வேண்டும்

.

இதன் பொருள் H துணைக்குழுவில்,

இதன் விளைவாக வரும் சமத்துவத்தை இடது காலத்தின் மூலம் காலத்தால் பெருக்குதல் , எங்களிடம் உள்ளது:

(9)

எங்கே

உறவு (9) பின்வரும் முடிவை எடுக்க அனுமதிக்கிறது.

உறுப்புகள் என்பதால்
எந்த உறுப்புக்கும் தன்னிச்சையாக தேர்ந்தெடுக்கப்படுகின்றன
மற்றும் எந்த உறுப்பு
ஒரு உறுப்பு உள்ளது

,

திருப்திகரமான உறவு (9).

கூடுதலாக, உறுப்பு
மற்றும் உறுப்பு
. இதன் காரணமாக, H ஐப் பொறுத்தமட்டில் G குழுவின் ஒவ்வொரு இடது கோசெட், அதே துணைக்குழு H ஐப் பொறுத்து G குழுவின் சில வலது கோசெட்டில் உள்ளது:

அதேபோல, ரிவர்ஸ் இன்க்லூஷனையும் காட்டலாம்

மற்றும் இது என்று பொருள்படும்

வரையறை 1. ஒரு குழு G இன் துணைக்குழு H அழைக்கப்படுகிறது சாதாரண வகுப்பான்அல்லது மாறாத துணைக்குழு, எச் என்ற துணைக்குழுவில் ஏதேனும் இரண்டு கோசெட்கள் g 1 H மற்றும் g 2 H எனில், தயாரிப்பு
தன்னிச்சையான கூறுகள்
இந்த வகுப்புகள் ஒரே கோசெட் வகுப்பைச் சேர்ந்தவை
(படம் 2).

அரிசி. 2- துணைக்குழு H என்பது குழு G இன் ஒரு சாதாரண துணைக்குழு ஆகும்.

முறையாக: துணைக்குழு H - சாதாரண வகுப்பான்குழுக்கள் , என்றால்:

பரிமாற்றக் குழுக்களில், ஒவ்வொரு துணைக்குழுவும் ஒரு சாதாரண வகுப்பான் (கூட்டல் செயல்பாட்டின் பரிமாற்றத் தன்மை காரணமாக).

ஒரு சாதாரண வகுப்பியின் கருத்தின் நடைமுறை பயன்பாட்டிற்கு, இன்னும் சில "கையாளுவதில் ஆக்கபூர்வமான" வரையறைகளைக் கருத்தில் கொள்வோம்.

வரையறை 2. G இன் துணைக்குழு H சாதாரண வகுப்பான்ஒரு குழு G இன் ஒவ்வொரு இடது கோசெட் இருந்தால் மட்டுமே
சரியான கூட்டுத்தொகையுடன் ஒத்துப்போகிறது
குழுக்கள் G மற்றும் H மற்றும் நேர்மாறாக.

முறையாக: துணைக்குழு H - சாதாரண வகுப்பான்குழு ஜி, என்றால்:

நிபந்தனை (12) என்பது தெளிவாகக் குறிக்கிறது:

எடுத்துக்காட்டுகள்.

1. எந்த குழுவிலும் G குழுவே
மற்றும் அலகு துணைக்குழு
அதன் இயல்பான வகுப்பிகள்: துணைக்குழுவின்படி G இன் இடது மற்றும் வலது கூட்டுத்தொகைகள்
ஒரு அருகிலுள்ள வகுப்பைக் கொண்டுள்ளது
, மற்றும் யூனிட் துணைக்குழு H இன் இடது (வலது) தொகுப்புகள் G குழுவின் அனைத்து கூறுகளையும் கொண்டிருக்கும்.

2. ஒவ்வொரு Abelian குழு G யிலும், அதன் ஒவ்வொரு துணைக்குழுவும் H ஒரு சாதாரண துணைக்குழுவாகும்.

3. நேர்மறை உண்மையான எண்களின் பெருக்கல் குழு
அனைத்து பூஜ்ஜியமற்ற உண்மையான எண்களின் பெருக்கல் குழுவின் ஒரு சாதாரண வகுப்பான்,

4. பூஜ்ஜியம் அல்லாத பகுத்தறிவு எண்களின் பெருக்கல் குழு
பூஜ்ஜியமற்ற உண்மையான எண்களின் பெருக்கல் குழுவின் சாதாரண வகுப்பான்

5. ஒரு பெருக்கல் குழுவில்
ஒருமை அல்லாத மெட்ரிக்குகள்
உண்மையான குணகங்களுடன் -வது வரிசை துணைக்குழு
ஒன்றுக்கு சமமான நிர்ணயம் கொண்ட மெட்ரிக்குகள்:

இந்த குழுவின் ஒரு சாதாரண வகுப்பான்.

உண்மையில், அடையாள அணி
, என்றால்

மற்றும்

- முறையே, குழுவின் இடது மற்றும் வலது கூட்டுத்தொகைகள்
-ஒருமை அல்லாத மெட்ரிக்குகள்
துணைக்குழுவின் மீது உண்மையான குணகங்களுடன் -வது வரிசை
- ஒன்றுக்கு சமமான தீர்மானிப்பான் கொண்ட மெட்ரிக்குகள்.

,

அந்த.
.

மறுபுறம், என்றால்

,

ஏனெனில்
அதனால் தான்

இதன் விளைவாக, அனைத்து மெட்ரிக்ஸையும் சமமான தீர்மானிப்பதன் மூலம் ஒரு கோசெட்டாக (இடது அல்லது வலது) தொகுப்பதன் மூலம் குழுவின் சிதைவைப் பெறுகிறோம்.
துணைக்குழு மூலம்
. பரிமாற்றம் அல்லாத குழுக்களும் துணைக்குழுக்களைக் கொண்டிருக்கலாம் என்பதை இந்த எடுத்துக்காட்டு காட்டுகிறது - சாதாரண வகுப்பிகள், இதற்கு இடது கோசெட்

சரியான கோசெட் உடன் ஒத்துப்போகிறது

துணைக்குழு எச்குழுக்கள் ஜிஒவ்வொரு தனிமத்திற்கும் சாதாரண வகுப்பி எனப்படும் gகுழுக்கள் ஜிதுணைக்குழு மூலம் அதன் இடது மற்றும் வலது இணைகள் எச்சமமானவை, அதாவது. gH=Hg.

தேற்றம் 2.5. துணைக்குழு எச்குழுக்கள் ஜிஇது ஒரு சாதாரண வகுப்பானாக இருந்தால் மட்டுமே எச்எதற்கும் gஇருந்து ஜிமற்றும் மஇருந்து எச்.

ஆதாரம்வெளிப்படையாக.

விடுங்கள் எச்ஒரு குழுவின் சாதாரண வகுப்பான் ஜி. கோசெட்களின் தொகுப்பில், குழு செயல்பாட்டால் தூண்டப்பட்ட பெருக்கல் செயல்பாட்டை அறிமுகப்படுத்துகிறோம். cosets தயாரிப்பு கீழ் aHமற்றும் bHஉறுப்புகளின் சாத்தியமான அனைத்து தயாரிப்புகளின் தொகுப்பையும் நாங்கள் புரிந்துகொள்வோம் aHஉறுப்புகளுக்கு bH. ஏனெனில் எச்ஒரு சாதாரண வகுப்பி, பின்னர் இந்த தயாரிப்புகள் அனைத்தும் கோசெட் வகுப்பில் உள்ளன ( ab)எச். இவ்வாறு, கோசெட்களின் தொகுப்பில் ஒரு செயல்பாடு அறிமுகப்படுத்தப்பட்டுள்ளது. இந்த செயல்பாடு துணை ( aHbH)cH=aH(bHcH), ஒரு நடுநிலை உறுப்பு உள்ளது எச், மற்றும் ஒவ்வொரு உறுப்புக்கும் aHஒரு தலைகீழ் உள்ளது a -1 எச். இதன் விளைவாக, அறிமுகப்படுத்தப்பட்ட செயல்பாட்டைப் பொறுத்தமட்டில் கோசெட்களின் தொகுப்பு, கோட்டியண்ட் குழு எனப்படும் ஒரு குழுவை உருவாக்குகிறது.

குழுக்களின் ஹோமோமார்பிசம்.

தனித்துவமான குழு காட்சி ஜிகுழுவிற்கு எச், செயல்பாட்டைப் பாதுகாக்கும், அழைக்கப்படுகிறது குழு ஓரினச்சேர்க்கை ஜிவி எச்.

ஐசோமார்பிசம் என்பது ஹோமோமார்பிஸத்தின் ஒரு சிறப்பு வழக்கு.

சொத்து 2.9. ஹோமோமார்பிஸத்தின் கீழ், குழுவின் நடுநிலை உறுப்பு ஜிநடுநிலை குழு உறுப்பில் காட்டப்படும் எச்.

ஆதாரம்சமத்துவத்திலிருந்து பின்பற்றுகிறது.

பல குழு கூறுகள் ஜி, ஒரு நடுநிலை உறுப்புக்கு வரைபடமாக்கப்பட்டது, இது ஹோமோமார்பிஸத்தின் கர்னல் என்று அழைக்கப்படுகிறது மற்றும் இது குறிக்கப்படுகிறது.

சொத்து 2.10.

ஆதாரம். அப்போதிருந்து.

சொத்து 2.11. ஹோமோமார்பிஸத்தின் கர்னல் குழுவின் ஒரு சாதாரண வகுப்பான் ஜி.

ஆதாரம். க்கு அஇருந்து ஜிமற்றும் பிமையத்தில் இருந்து உண்மை, அதாவது.

பல குழு கூறுகள் எச், அவை உறுப்புகளின் படங்கள் ஜி, படங்களின் தொகுப்பு என்று அழைக்கப்படுகிறது மற்றும் குறிக்கிறது.

சொத்து 2.12. படங்களின் தொகுப்பு ஒரு துணைக்குழு எச்.

ஆதாரம்வெளிப்படையாக.

தேற்றம் 2.6. காரணி குழு ஐசோமார்பிக் ஆகும்.

ஆதாரம். கடிதப் பரிமாற்றம் ஒன்றுக்கு ஒன்று மற்றும் செயல்பாட்டைப் பாதுகாக்கிறது, எனவே இது ஒரு ஐசோமார்பிஸத்தை வரையறுக்கிறது மற்றும் .

தேற்றம் 2.7. எந்த சாதாரண வகுக்கவும் எச்குழுக்கள் ஜிகர்னல் சமமாக இருக்கும் ஒரு ஹோமோமார்பிசம் உள்ளது எச். குறிப்பாக, இருந்து அத்தகைய ஒரு homomorphism ஜிவி ஜி/எச்இருக்கிறது .

ஆதாரம்வெளிப்படையாக.

சாதாரண வரிசை

ஹோமோமார்பிஸம் பற்றிய இரண்டு கோட்பாடுகளை நிரூபிப்போம்.

தேற்றம் 2.8. விடுங்கள் எச்சாதாரண குழு வகுப்பான் ஜிமற்றும் பி- துணைக்குழு ஜி. பின்னர் சாதாரண வகுத்தல் பிமற்றும்

ஆதாரம். இருக்கட்டும். பின்னர் இருந்து எச்சாதாரண வகுப்பான் ஜி, மற்றும் அனைத்து கூறுகளும் இருந்து பி. எனவே, இது ஒரு சாதாரண வகுப்பான் பி. போட்டி ஒன்றுக்கு ஒன்று மற்றும் செயல்பாட்டைப் பாதுகாக்கிறது. தேற்றம் நிரூபிக்கப்பட்டுள்ளது.

தேற்றம் 2.9. விடுங்கள் பிஒரு சாதாரண வகுப்பி மற்றும் . பிறகு டி- சாதாரண வகுப்பான் ஜிமற்றும் .

ஆதாரம். எங்கே என்று பார்ப்போம். இருந்து , பின்னர் , மற்றும், அர்த்தம் டி- சாதாரண வகுப்பான் ஜி. கடிதப் பரிமாற்றம் ஒன்றுக்கு ஒன்று, ஏனெனில் மற்றும் செயல்பாட்டைச் சேமிக்கிறது.

ஒரு குழு தன்னைத் தவிர வேறு சாதாரண வகுத்தல் மற்றும் அலகு துணைக்குழு இல்லாமல் இருந்தால் எளிமையானது என்று அழைக்கப்படுகிறது.

ஒரு குழுவின் ஒரு சாதாரண தொடர் என்பது துணைக்குழுக்களின் வரிசையாகும், இதில் ஒவ்வொரு அடுத்தடுத்து முந்தைய ஒரு வழக்கமான வகுப்பான் ஆகும். ஒரு சாதாரண தொடரின் அனைத்து குழுக்களும் ஒரு சாதாரண தொடரில் இருந்தால், இரண்டாவது சாதாரண தொடரானது முதல் சாதாரண தொடரை ஒடுக்குவதன் மூலம் பெறப்படும் என்று கூறப்படுகிறது.

சுருக்க முடியாத மறுநிகழ்வுகள் இல்லாத ஒரு சாதாரண தொடர் தொகுப்பு எனப்படும்.

ஒரு சாதாரண தொடருக்கான காரணிகள் வரையறுக்கப்படுகின்றன . முதல் தொடரின் அனைத்து காரணிகளும் ஒரு குறிப்பிட்ட வரிசையில் மறுசீரமைக்கப்பட்ட இரண்டாவது தொடரின் காரணிகளுக்கு ஐசோமார்பிக் என்றால் இரண்டு சாதாரண தொடர்கள் ஐசோமார்பிக் என்று அழைக்கப்படுகின்றன.

சொத்து 2.13. சாதாரண தொடர்கள் ஐசோமார்ஃபிக் என்றால், முதல் தொடரின் ஒவ்வொரு ஒடுக்கத்திற்கும், இரண்டாவது தொடரின் ஐசோமார்ஃபிக் ஒடுக்கத்தைக் காணலாம்.

ஆதாரம்.துணைக்குழுக்களுக்கு இடையே புதிய துணைக்குழுக்கள் தோன்றியுள்ளன என்று வைத்துக் கொள்வோம். ஏனெனில் எனவே, காரணிகள் தொடர்புடைய துணைக்குழுக்களுக்கு ஐசோமார்பிக் ஆகும். தொடர்புடைய துணைக்குழுவால் குறிப்போம். குழுக்களின் வரிசையை வரையறுப்போம், எங்கே நான்=1,…,டி. மேலே நிரூபிக்கப்பட்ட தேற்றத்தின்படி. எனவே, குழுக்களால் இரண்டாவது வரிசையின் சுருக்கமானது ஐசோமார்பிக் ஆகும். சொத்து நிரூபிக்கப்பட்டுள்ளது.