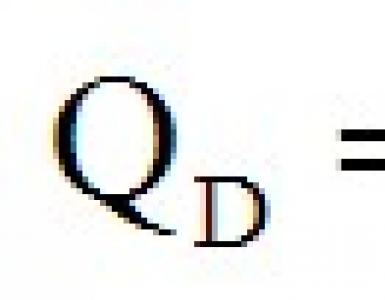Typy postupov zhlukovej analýzy. I.A

Pri veľkom počte pozorovaní nie sú vhodné hierarchické metódy zhlukovej analýzy. V takýchto prípadoch sa využívajú nehierarchické metódy založené na delení, čo sú iteratívne metódy fragmentácie pôvodnej populácie. Počas procesu delenia sa vytvárajú nové zhluky, kým nie je splnené pravidlo zastavenia.

Takéto nehierarchické zhlukovanie pozostáva z rozdelenia súboru údajov do určitého počtu jednotlivých zhlukov. Sú dva prístupy. Prvým je určenie hraníc zhlukov ako najhustejších oblastí vo viacrozmernom priestore zdrojových údajov, t.j. definovanie zhluku, kde dochádza k veľkej „kondenzácii bodov“. Druhým prístupom je minimalizovať mieru rozdielu medzi objektmi

algoritmus k-means

Najbežnejšou nehierarchickou metódou je algoritmus k-means, nazývaný aj rýchla zhluková analýza. Kompletný popis algoritmu možno nájsť v Hartigan a Wong (1978). Na rozdiel od hierarchických metód, ktoré nevyžadujú predbežné predpoklady o počte zhlukov, aby bolo možné túto metódu použiť, je potrebné mať hypotézu o najpravdepodobnejšom počte zhlukov.

Algoritmus k-means konštruuje k zhlukov umiestnených v najväčších možných vzdialenostiach od seba. Hlavným typom problémov, ktoré algoritmus k-means rieši, je prítomnosť predpokladov (hypotéz) týkajúcich sa počtu zhlukov, ktoré by sa mali čo najviac líšiť. Výber k môže byť založený na predchádzajúcom výskume, teoretických úvahách alebo intuícii.

Všeobecná myšlienka algoritmu: daný pevný počet k pozorovacích zhlukov sa porovnáva so zhlukmi tak, aby sa priemery v klastri (pre všetky premenné) od seba čo najviac líšili.

Popis algoritmu

Počiatočná distribúcia objektov do zhlukov. Vyberie sa číslo k av prvom kroku sa tieto body považujú za „stredy“ zhlukov. Každý zhluk zodpovedá jednému centru.
Výber počiatočných ťažísk možno vykonať nasledovne:
- výber k-pozorovaní na maximalizáciu počiatočnej vzdialenosti;
- náhodný výber k-pozorovaní;
- výber prvých k-pozorovaní.
Výsledkom je, že každý objekt je priradený ku konkrétnemu zhluku.
Iteračný proces. Vypočítajú sa stredy zhlukov, ktoré sa potom použijú na výpočet súradnicových priemerov zhlukov. Objekty sa opäť prerozdelia.
Proces výpočtu centier a prerozdeľovania objektov pokračuje, kým nie je splnená jedna z podmienok:
- centrá klastrov sa stabilizovali, t.j. všetky pozorovania patria do klastra, do ktorého patrili pred aktuálnou iteráciou;
- počet iterácií sa rovná maximálnemu počtu iterácií.

Na obr. Obrázok 14.1 ukazuje príklad toho, ako funguje algoritmus k-means pre k rovné dvom.

Obrázok 1 - Príklad algoritmu k-means (k=2)

Výber počtu klastrov je zložitý problém. Ak neexistujú žiadne predpoklady týkajúce sa tohto počtu, odporúča sa vytvoriť 2 zhluky, potom 3, 4, 5 atď., Porovnaním získaných výsledkov.

Kontrola kvality klastrovania

Po obdržaní výsledkov klastrovej analýzy k-means by ste mali skontrolovať správnosť klastrovania (t. j. posúdiť, nakoľko sa zhluky navzájom líšia). Na tento účel sa vypočítajú priemerné hodnoty pre každý klaster. Dobré zhlukovanie by malo produkovať veľmi odlišné prostriedky pre všetky merania, alebo aspoň pre väčšinu z nich.

Výhody algoritmu k-means:

jednoduchosť použitia;
rýchlosť používania;
zrozumiteľnosť a transparentnosť algoritmu.

Nevýhody algoritmu k-means:

Algoritmus je príliš citlivý na odľahlé hodnoty, ktoré môžu skresliť priemer. Možným riešením tohto problému je použitie modifikácie algoritmu - k-mediánového algoritmu;
algoritmus môže byť pomalý vo veľkých databázach. Možným riešením tohto problému je použitie vzorkovania údajov.

Algoritmus PAM (partitioning around Medoids).

PAM je modifikáciou algoritmu k-means, algoritmu k-medoids.

Algoritmus je menej citlivý na šum a odľahlé hodnoty v údajoch ako algoritmus k-means, pretože medián je menej ovplyvnený odľahlými hodnotami.

PAM je účinný pre malé databázy, ale nemal by sa používať pre veľké súbory údajov. Predbežné zmenšenie rozmerov

Pozrime sa na príklad. Existuje databáza klientov spoločnosti, ktorá by mala byť rozdelená do homogénnych skupín. Každý klient je opísaný pomocou 25 premenných. Použitie takého veľkého množstva premenných vedie k identifikácii zhlukov s fuzzy štruktúrou. V dôsledku toho je pre analytika pomerne ťažké interpretovať výsledné zhluky.

Zrozumiteľnejšie a transparentnejšie výsledky zhlukovania možno získať, ak sa namiesto súboru počiatočných premenných použijú niektoré zovšeobecnené premenné alebo kritériá, ktoré obsahujú komprimované informácie o vzťahoch medzi premennými. Tie. Problémom je zníženie rozmerov údajov. Dá sa vyriešiť rôznymi metódami; Jednou z najbežnejších je faktorová analýza. Pozrime sa na to podrobnejšie.

Faktorová analýza

Faktorová analýza je metóda používaná na štúdium vzťahov medzi hodnotami premenných.

Faktorová analýza má vo všeobecnosti dva ciele:

zníženie počtu premenných;
klasifikácia premenných - určenie štruktúry vzťahov medzi premennými.

Faktorová analýza sa teda môže použiť na riešenie problémov znižovania rozmerov údajov alebo na riešenie problémov klasifikácie.

Kritériá alebo hlavné faktory identifikované ako výsledok faktorovej analýzy obsahujú v komprimovanej forme informácie o existujúcich vzťahoch medzi premennými. Tieto informácie nám umožňujú získať lepšie výsledky zhlukovania a lepšie vysvetliť sémantiku zhlukov. Faktory samotné môžu mať určitý význam.

Pomocou faktorovej analýzy sa veľké množstvo premenných redukuje na menší počet nezávislých ovplyvňujúcich veličín, ktoré sa nazývajú faktory.

Faktor v „komprimovanej“ forme obsahuje informácie o niekoľkých premenných. Premenné, ktoré medzi sebou vysoko korelujú, sa spájajú do jedného faktora. Výsledkom faktorovej analýzy sú komplexné faktory, ktoré čo najúplnejšie vysvetľujú vzťahy medzi uvažovanými premennými.

V prvom kroku faktorovej analýzy sa štandardizujú hodnoty premenných, ktorých potreba bola diskutovaná v predchádzajúcej prednáške.

Faktorová analýza je založená na hypotéze, že analyzované premenné sú nepriamym prejavom relatívne malého počtu určitých skrytých faktorov.

Faktorová analýza je súbor metód zameraných na identifikáciu a analýzu skrytých závislostí medzi pozorovanými premennými. Skryté závislosti sa nazývajú aj latentné závislosti.

Jedna z metód faktorovej analýzy – metóda hlavných komponentov – je založená na predpoklade, že faktory sú na sebe nezávislé.

Iteratívne klastrovanie v SPSSŠtatistické balíky zvyčajne implementujú široký arzenál metód, ktoré vám umožňujú najprv zmenšiť rozmer súboru údajov (napríklad pomocou faktorovej analýzy) a potom samotné zhlukovanie (napríklad pomocou metódy rýchlej klastrovej analýzy). Zoberme si túto možnosť pre klastrovanie v SPSS.
Na zníženie dimenzionality zdrojových údajov použijeme faktorovú analýzu. Ak to chcete urobiť, vyberte z ponuky: Analyze/Data Reduction/Factor:
Pomocou tlačidla Extrakcia: vyberte metódu extrakcie. Predvolenú analýzu hlavných komponentov ponecháme vybratú, ako je uvedené vyššie. Zvoliť by ste si mali aj metódu rotácie – vyberme si jednu z najobľúbenejších – metódu varimax. Ak chcete uložiť hodnoty faktorov ako premenné, na karte „Hodnoty“ musíte začiarknuť políčko „Uložiť ako premenné“.

Výsledkom tohto postupu je, že používateľ dostane správu „Vysvetlená celková odchýlka“, ktorá zobrazuje počet vybraných faktorov - to sú tie komponenty, ktorých vlastné hodnoty presahujú jednu.

Získané hodnoty faktorov, ktoré sa zvyčajne nazývajú fakt1_1, fakt1_2 atď., sa používajú na vykonanie zhlukovej analýzy pomocou metódy k-means. Ak chcete vykonať rýchlu analýzu klastrov, vyberte z ponuky:

Analyze/Classify/K-Means Cluster: (Zhluková analýza pomocou metódy k-means).

V dialógovom okne K Means Cluster Analysis musíte umiestniť premenné faktora fact1_1, fact1_2 atď. v oblasti testovaných premenných. Tu musíte zadať počet klastrov a počet iterácií.

V dôsledku tohto postupu získame správu zobrazujúcu hodnoty stredov vytvorených zhlukov, počet pozorovaní v každom zhluku, ako aj ďalšie informácie špecifikované používateľom.

Algoritmus k-means teda rozdeľuje pôvodný súbor údajov do daného počtu zhlukov. Aby ste mohli vizualizovať získané výsledky, mali by ste použiť jeden z grafov, napríklad bodový graf. Tradičná vizualizácia je však možná pre obmedzený počet dimenzií, pretože, ako je známe, človek dokáže vnímať len trojrozmerný priestor. Ak teda analyzujeme viac ako tri premenné, mali by sme na prezentáciu informácií použiť špeciálne multidimenzionálne metódy, o ktorých bude reč v niektorej z nasledujúcich prednášok kurzu.

Metódy iteračného klastrovania sa líšia výberom nasledujúcich parametrov:

štartovací bod;
pravidlo pre vytváranie nových klastrov;
pravidlo zastavenia.

Výber metódy klastrovania závisí od množstva údajov a od toho, či je potrebné pracovať s viacerými typmi údajov súčasne.

Napríklad v SPSS, ak je potrebné pracovať s kvantitatívnymi (napríklad príjem) aj kategorickými (napríklad rodinný stav) premennými, a tiež ak je objem údajov dostatočne veľký, metóda dvojstupňovej klastrovej analýzy sa používa, čo je škálovateľná analýza klastrovacích procedúr, ktorá umožňuje pracovať s dátami rôznych typov. Na tento účel sa v prvej fáze práce záznamy vopred zoskupia do veľkého počtu podskupín. V druhej fáze sa výsledné podskupiny zoskupia do požadovaného počtu. Ak toto množstvo nie je známe, postup ho automaticky určí. Pomocou tohto postupu môže pracovník banky napríklad identifikovať skupiny ľudí, pričom súčasne využíva ukazovatele ako vek, pohlavie a úroveň príjmu. Získané výsledky umožňujú identifikovať klientov s rizikom nesplácania úveru.

Vo všeobecnosti sú všetky fázy klastrovej analýzy prepojené a rozhodnutia prijaté v jednej z nich určujú akcie v nasledujúcich fázach.

Analytik sa musí rozhodnúť, či použije všetky pozorovania alebo vylúči niektoré údaje alebo vzorky zo súboru údajov.

Výber metrík a spôsob štandardizácie zdrojových údajov.

Určenie počtu klastrov (pre iteračnú klastrovú analýzu).

Definícia metódy klastrovania (pravidlá asociácie alebo spojenia).

Podľa mnohých odborníkov je pri určovaní tvaru a špecifickosti zhlukov rozhodujúci výber metódy zhlukovania.

Analýza výsledkov zhlukovania. Táto fáza zahŕňa riešenie nasledujúcich otázok: je výsledné rozdelenie do zhlukov náhodné; či je oddiel spoľahlivý a stabilný na čiastkových vzorkách údajov; existuje vzťah medzi výsledkami zoskupovania a premennými, ktoré neboli zahrnuté do procesu zoskupovania; Je možné interpretovať získané výsledky zhlukovania?

Kontrola výsledkov klastrovania. Výsledky klastrovania sa musia overiť aj pomocou formálnych a neformálnych metód. Formálne metódy závisia od metódy použitej na zhlukovanie. Neformálne zahŕňajú nasledujúce postupy na kontrolu kvality klastrovania:

analýza výsledkov zhlukovania získaných na určitých vzorkách súboru údajov;
krížová validácia;
vykonávanie zhlukovania pri zmene poradia pozorovaní v súbore údajov;
vykonávanie zhlukovania pri odstraňovaní niektorých pozorovaní;
klastrovanie na malých vzorkách.

Jednou z možností kontroly kvality zhlukovania je použitie viacerých metód a porovnanie získaných výsledkov. Neprítomnosť podobnosti neznamená, že výsledky sú nesprávne, ale prítomnosť podobných skupín sa považuje za znak kvalitného zhlukovania.

Ťažkosti a problémy, ktoré môžu vzniknúť pri aplikácii zhlukovej analýzy

Ako každá iná metóda, aj metódy klastrovej analýzy majú určité slabé stránky, t.j. určité ťažkosti, problémy a obmedzenia.

Pri vykonávaní klastrovej analýzy by sa malo vziať do úvahy, že výsledky klastrovania závisia od kritérií na rozdelenie súboru počiatočných údajov. Pri zmenšovaní rozmeru dát môže dochádzať k určitým skresleniam, v dôsledku zovšeobecňovania môže dôjsť k strate niektorých individuálnych charakteristík objektov.

Pred vykonaním klastrovania je potrebné zvážiť množstvo zložitostí.

Ťažkosti pri výbere charakteristík, na základe ktorých sa zhlukovanie vykonáva. Unáhlený výber vedie k nedostatočnému rozdeleniu do zhlukov a v dôsledku toho k nesprávnemu riešeniu problému.
Ťažkosti pri výbere metódy klastrovania. Tento výber si vyžaduje dobrú znalosť metód a predpokladov na ich použitie. Na testovanie účinnosti konkrétnej metódy v určitej tematickej oblasti je vhodné použiť nasledujúci postup: zvážiť niekoľko a priori odlišných skupín a náhodne zmiešať ich zástupcov medzi sebou. Ďalej sa vykoná zhlukovanie, aby sa obnovilo pôvodné rozdelenie do zhlukov. Percento zhody objektov v identifikovaných a počiatočných skupinách je indikátorom účinnosti metódy.
Problém výberu počtu klastrov. Ak neexistujú žiadne informácie o možnom počte zhlukov, je potrebné vykonať sériu experimentov a ako výsledok skúšania rôznych počtov zhlukov vybrať ich optimálny počet.
Problém interpretácie výsledkov zhlukovania. Tvar zhlukov je vo väčšine prípadov určený výberom spôsobu spájania. Malo by sa však vziať do úvahy, že špecifické metódy majú tendenciu vytvárať zhluky určitých tvarov, aj keď v skúmanom súbore údajov v skutočnosti žiadne zhluky nie sú.

Porovnávacia analýza hierarchických a nehierarchických metód zhlukovania

Pred uskutočnením klastrovania môže mať analytik otázku, ktorú skupinu metód klastrovej analýzy uprednostniť. Pri výbere medzi hierarchickými a nehierarchickými metódami je potrebné vziať do úvahy ich nasledujúce vlastnosti.

Nehierarchické metódy odhaľujú vyššiu stabilitu vzhľadom na šum a odľahlé hodnoty, nesprávny výber metrík a zahrnutie nevýznamných premenných do súboru zúčastňujúceho sa zhlukovania. Cena, ktorú treba zaplatiť za tieto výhody metódy, je slovo „a priori“. Analytik musí vopred určiť počet klastrov, počet iterácií alebo pravidlo zastavenia a niektoré ďalšie parametre klastrovania. To je obzvlášť ťažké pre začiatočníkov.

Ak neexistujú žiadne predpoklady týkajúce sa počtu zhlukov, odporúča sa použiť hierarchické algoritmy. Ak to však veľkosť vzorky neumožňuje, možnou cestou je vykonať sériu experimentov s rôznym počtom zhlukov, napríklad začať deliť súbor údajov na dve skupiny a postupným zvyšovaním ich počtu porovnávať výsledky. Vďaka tejto „variácii“ výsledkov sa dosiahne pomerne veľká flexibilita zoskupovania.

Hierarchické metódy na rozdiel od nehierarchických odmietajú určiť počet zhlukov, ale budujú kompletný strom vnorených zhlukov.

Ťažkosti metód hierarchického zhlukovania: obmedzenie veľkosti súboru údajov; výber miery blízkosti; nepružnosť výsledných klasifikácií.

Výhodou tejto skupiny metód v porovnaní s nehierarchickými metódami je ich viditeľnosť a možnosť získať detailné pochopenie štruktúry údajov.

Pri použití hierarchických metód je možné pomerne jednoducho identifikovať odľahlé hodnoty v súbore údajov a v dôsledku toho zlepšiť kvalitu údajov. Tento postup je základom dvojkrokového klastrovacieho algoritmu. Takýto súbor údajov možno neskôr použiť na vykonávanie nehierarchického zoskupovania.

Je tu ešte jeden aspekt, ktorý už bol spomenutý v tejto prednáške. Ide o zhlukovanie celého súboru údajov alebo jeho vzorky. Tento aspekt je podstatný pre obe skupiny posudzovaných metód, ale je kritickejší pre hierarchické metódy. Hierarchické metódy nedokážu pracovať s veľkými súbormi údajov a použitie nejakého vzorkovania, napr. časti údajov by mohli umožniť použitie týchto metód.

Výsledky zoskupovania nemusia mať dostatočné štatistické opodstatnenie. Na druhej strane pri riešení zhlukovacích problémov je akceptovateľná neštatistická interpretácia získaných výsledkov, ako aj pomerne veľká rôznorodosť variantov koncepcie klastra. Táto neštatistická interpretácia umožňuje analytikovi získať výsledky zhlukovania, ktoré ho uspokojujú, čo je často ťažké pri použití iných metód.

Nové algoritmy a niektoré modifikácie algoritmov zhlukovej analýzy

Metódy, o ktorých sme hovorili v tejto a predchádzajúcich prednáškach, sú „klasikou“ zhlukovej analýzy. Až donedávna bola hlavným kritériom, podľa ktorého sa hodnotil klastrovací algoritmus, kvalita klastrovania: predpokladalo sa, že celý súbor údajov sa zmestí do pamäte RAM.

Teraz sa však v dôsledku objavenia sa ultra veľkých databáz objavili nové požiadavky, ktoré musí klastrovací algoritmus spĺňať. Hlavným, ako už bolo spomenuté v predchádzajúcich prednáškach, je škálovateľnosť algoritmu.

Všimnime si aj ďalšie vlastnosti, ktoré musí spĺňať klastrovací algoritmus: nezávislosť výsledkov od poradia vstupných údajov; nezávislosť parametrov algoritmu od vstupných údajov.

Nedávno došlo k aktívnemu vývoju nových klastrovacích algoritmov schopných spracovávať ultra veľké databázy. Zameriavajú sa na škálovateľnosť. Takéto algoritmy zahŕňajú súhrnnú klastrovú reprezentáciu, ako aj výber a použitie dátových štruktúr podporovaných základným DBMS.

Boli vyvinuté algoritmy, v ktorých sú metódy hierarchického zhlukovania integrované s inými metódami. Takéto algoritmy zahŕňajú: BIRCH, CURE, CHAMELEON, ROCK.

Algoritmus BIRCH (vyvážené iteračné znižovanie a klastrovanie pomocou hierarchií)

Algoritmus navrhol Tian Zang a jeho kolegovia.

Vďaka zovšeobecneným reprezentáciám klastrov sa rýchlosť klastrovania zvyšuje, pričom algoritmus je vysoko škálovateľný.

Tento algoritmus implementuje dvojstupňový proces klastrovania.

Počas prvej etapy sa vytvorí predbežný súbor klastrov. V druhej fáze sa na identifikované klastre aplikujú ďalšie klastrovacie algoritmy - vhodné pre prácu v RAM.

Nasledujúca analógia popisuje tento algoritmus. Ak si každý dátový prvok predstavujeme ako guľôčku ležiacu na povrchu stola, potom zhluky guľôčok možno „nahradiť“ tenisovými loptičkami a pristúpiť k podrobnejšiemu štúdiu zhlukov tenisových loptičiek. Počet guľôčok môže byť dosť veľký, ale priemer tenisových loptičiek môže byť zvolený tak, že v druhej fáze je možné pomocou tradičných zhlukových algoritmov určiť skutočný komplexný tvar zhlukov.

Algoritmus WaveCluster

WaveCluster je zhlukovací algoritmus založený na vlnových transformáciách. Na začiatku algoritmu sú údaje zovšeobecnené aplikáciou viacrozmernej mriežky na dátový priestor. V ďalších krokoch algoritmu sa neanalyzujú jednotlivé body, ale zovšeobecnené charakteristiky bodov spadajúcich do jednej bunky mriežky. V dôsledku tohto zovšeobecnenia sa potrebné informácie zmestia do pracovnej pamäte. V nasledujúcich krokoch algoritmus aplikuje vlnovú transformáciu na zovšeobecnené dáta na identifikáciu zhlukov.

Hlavné vlastnosti WaveCluster:

zložitosť implementácie;
algoritmus dokáže detekovať zhluky ľubovoľných tvarov;
algoritmus nie je citlivý na šum;
Algoritmus je použiteľný len pre nízkorozmerné dáta.

Algoritmus CLARA (Zhlukovanie veľkých aplikácií)

Algoritmus CLARA vyvinuli Kaufmann a Rousseeuw v roku 1990 na zoskupovanie údajov vo veľkých databázach. Tento algoritmus je zabudovaný do štatistických analytických balíkov, ako je napríklad S+.

Stručne načrtneme podstatu algoritmu. Algoritmus CLARA získava veľa vzoriek z databázy. Klastrovanie sa aplikuje na každú zo vzoriek a algoritmus poskytuje najlepšie zoskupovanie.

Pre veľké databázy je tento algoritmus efektívnejší ako algoritmus PAM. Účinnosť algoritmu závisí od súboru údajov vybratého ako vzorka. Dobré klastrovanie vo vybranej množine nemusí produkovať dobré klastrovanie v celej množine údajov.

Algoritmy Clarans, CURE, DBScan

Claransov algoritmus (Clustering Large Applications based on RANdomized Search) formuluje problém zhlukovania ako náhodné vyhľadávanie v grafe. Výsledkom činnosti tohto algoritmu je, že zbierka uzlov grafu predstavuje rozdelenie súboru údajov do používateľom definovaného počtu zhlukov. „Kvalita“ výsledných zhlukov sa určuje pomocou funkcie kritéria. Algoritmus Clarans triedi všetky možné oddiely súboru údajov, aby našiel prijateľné riešenie. Hľadanie riešenia sa zastaví v uzle, kde je dosiahnuté minimum medzi vopred určeným počtom lokálnych miním.

Medzi nové škálovateľné algoritmy môžeme zaznamenať aj algoritmus CURE - hierarchický zhlukovací algoritmus a algoritmus DBScan, kde je koncept klastra formulovaný pomocou konceptu hustoty.

Hlavnou nevýhodou algoritmov BIRCH, Clarans, CURE, DBScan je skutočnosť, že vyžadujú nastavenie určitých prahových hodnôt hustoty bodov, čo nie je vždy prijateľné. Tieto obmedzenia sú spôsobené tým, že opísané algoritmy sú zamerané na ultra veľké databázy a nemôžu využívať veľké výpočtové zdroje.

Mnoho výskumníkov teraz aktívne pracuje na škálovateľných metódach, ktorých hlavnou úlohou je prekonať nedostatky súčasných algoritmov.

Zhluková analýza (CLA) je súborom viacrozmerných klasifikačných metód, ktorých účelom je vytvárať skupiny (zhluky) podobných objektov. Na rozdiel od tradičných zoskupení uvažovaných vo všeobecnej teórii štatistiky, ClA vedie k rozdeleniu do skupín, ktoré zohľadňujú všetky charakteristiky zoskupovania súčasne.

Metódy KLA vám umožňujú vyriešiť nasledujúce problémy:

— klasifikácia objektov s prihliadnutím na mnohé charakteristiky;

— kontrola predpokladov o prítomnosti nejakej štruktúry v skúmanom súbore objektov, t.j. hľadať existujúcu štruktúru;

— vytvorenie nových klasifikácií pre nedostatočne študované javy, keď je potrebné zistiť prítomnosť súvislostí v rámci populácie a pokúsiť sa do nej vniesť štruktúru.

Na písanie formalizovaných algoritmov KLA sa používajú nasledujúce konvencie:

– súbor pozorovacích objektov;

– i-té pozorovanie v priestore m-rozmerných prvkov ();

– vzdialenosť medzi -tým a -tým objektom;

– normalizované hodnoty pôvodných premenných;

– matica vzdialeností medzi objektmi.

Na implementáciu akejkoľvek metódy KLA je potrebné zaviesť pojem „podobnosť objektov“. Navyše, počas procesu klasifikácie by mal každý klaster obsahovať objekty, ktoré sú si navzájom najviac podobné z hľadiska pozorovaných premenných.

Na kvantifikáciu podobnosti sa zavádza pojem metriky. Každý objekt je popísaný -vlastnosťami a reprezentovaný ako bod v -rozmernom priestore. Podobnosť alebo rozdiel medzi klasifikovanými objektmi sa určuje v závislosti od metrickej vzdialenosti medzi nimi. Zvyčajne sa používajú tieto miery vzdialenosti medzi objektmi:

— Euklidovská vzdialenosť ;

— vážená euklidovská vzdialenosť ;

— vzdialenosť mestského bloku ;

— vzdialenosť Mahalanobis,

kde je vzdialenosť medzi tým a tým objektom;

, sú hodnoty -premennej a -tého a -tého objektu;

, – vektory premenných hodnôt pre -tý a -tý objekt;

– všeobecná kovariančná matica;

– váha priradená tej premennej.

Všetky metódy KLA možno rozdeliť do dvoch skupín: hierarchické (aglomeratívne a divízne) a iteračné (metóda priemerov, metóda hľadania kondenzácií).

Hierarchická zhluková analýza. Zo všetkých metód klastrovej analýzy je najbežnejší aglomeračný klasifikačný algoritmus. Podstatou agrogritu je, že v prvom kroku je každý vzorový objekt považovaný za samostatný zhluk. Proces zlučovania zhlukov prebieha postupne: na základe matice vzdialenosti alebo matice podobnosti sa kombinujú najbližšie objekty. Ak má matica vzdialenosti na začiatku rozmer (), potom sa celý proces zlučovania dokončí v krokoch (). V dôsledku toho budú všetky objekty spojené do jedného zhluku.

Sekvenciu asociácie možno znázorniť ako dendrogram, znázornený na obrázku 3.1. Dendrogram ukazuje, že v prvom kroku sa druhý a tretí objekt spojili do jedného zhluku so vzdialenosťou medzi nimi 0,15. V druhom kroku sa k nim pripojil prvý objekt. Vzdialenosť od prvého objektu k zhluku obsahujúcemu druhý a tretí objekt je 0,3 atď.

Mnohé metódy hierarchickej klastrovej analýzy sa líšia vo svojich kombinovaných (podobných) algoritmoch, z ktorých najbežnejšie sú: metóda jedného prepojenia, metóda úplného prepojenia, metóda priemerného prepojenia a Wardova metóda.

Metóda úplných spojení - nový objekt je zaradený do zhluku iba vtedy, ak podobnosť medzi všetkými objektmi nie je menšia ako určitá úroveň podobnosti (obrázok 1.3).

Priemerná metóda pripojenia – keď je nový objekt zahrnutý do existujúceho klastra, vypočíta sa priemerná hodnota miery podobnosti, ktorá sa potom porovná so špecifikovanou prahovou úrovňou. Ak hovoríme o kombinácii dvoch zhlukov, potom sa vypočíta miera podobnosti medzi ich centrami a porovná sa s danou prahovou hodnotou. Uvažujme geometrický príklad s dvoma klastrami (obrázok 1.4).

Obrázok 1.4. Kombinácia dvoch klastrov pomocou metódy priemerného prepojenia:

Ak miera podobnosti medzi centrami klastrov () nie je menšia ako daná úroveň, klastre sa spoja do jedného.

Wardova metóda – v prvom kroku sa každý zhluk skladá z jedného objektu. Na začiatku sa spoja dva najbližšie klastre. Pre nich sa určia priemerné hodnoty každej charakteristiky a vypočíta sa súčet štvorcových odchýlok

, (1.1)

kde je číslo klastra, je číslo objektu, je číslo funkcie; – počet znakov charakterizujúcich každý objekt; – počet objektov v -mklastri.

Následne sa v každom kroku algoritmu kombinujú tie objekty alebo zhluky, ktoré poskytujú najmenší prírastok hodnoty.

Výsledkom Wardovej metódy sú zhluky približne rovnakej veľkosti s minimálnou vnútroklastrovou variáciou.

Algoritmus hierarchickej klastrovej analýzy možno reprezentovať ako postupnosť procedúr:

- normalizácia počiatočných hodnôt premenných;

— výpočet matice vzdialeností alebo matice mier podobnosti;

— určenie dvojice najbližších objektov (zhlukov) a ich kombinácie podľa zvoleného algoritmu;

— opakovanie prvých troch postupov, kým sa všetky objekty neskombinujú do jedného zhluku.

Miera podobnosti pre kombináciu dvoch klastrov sa určuje nasledujúcimi metódami:

— metóda „najbližší sused“ – miera podobnosti medzi zhlukami sa posudzuje podľa miery podobnosti medzi najpodobnejšími (najbližšími) objektmi týchto zhlukov;

— metóda „vzdialeného suseda“ – stupeň podobnosti sa hodnotí podľa stupňa podobnosti medzi najvzdialenejšími (nepodobnými) objektmi zhlukov;

- priemerná metóda spojenia - stupeň podobnosti sa odhaduje ako priemerná hodnota stupňov podobnosti medzi objektmi zhlukov;

- mediánová metóda spojenia - vzdialenosť medzi ľubovoľným zhlukom S a novým zhlukom, ktorá bola získaná ako výsledok spojenia zhlukov p a q, je definovaná ako vzdialenosť od stredu zhluku S k stredu segmentu spájajúceho stredy zhlukov. zhluky p a q.

Metóda hľadania kondenzácií. Jednou z iteratívnych metód klasifikácie je algoritmus klastrového vyhľadávania. Podstatou iteračného algoritmu tejto metódy je použitie hypersféry daného polomeru, ktorá sa pohybuje v priestore klasifikačných znakov za účelom hľadania lokálnych koncentrácií objektov.

Metóda hľadania kondenzácií vyžaduje v prvom rade výpočet matice vzdialeností (alebo matice mier podobnosti) medzi objektmi a výber počiatočného stredu gule. Typicky je v prvom kroku stredom gule objekt (bod), v ktorého bezprostrednej blízkosti sa nachádza najväčší počet susedov. Na základe daného polomeru gule (R) sa určí množina bodov spadajúcich do tejto gule, pre ktoré sa vypočítajú súradnice stredu (vektor priemerných hodnôt znakov).

Keď ďalší prepočet súradníc stredu gule povedie k rovnakému výsledku ako v predchádzajúcom kroku, pohyb gule sa zastaví a body, ktoré do nej spadajú, vytvoria zhluk a sú vylúčené z ďalšieho procesu zhlukovania. Vyššie uvedené postupy sa opakujú pre všetky zostávajúce body. Algoritmus je dokončený v konečnom počte krokov a všetky body sú rozdelené do zhlukov. Počet vytvorených zhlukov nie je vopred známy a silne závisí od polomeru gule.

Na posúdenie stability výslednej priečky je vhodné niekoľkokrát zopakovať proces zhlukovania pre rôzne hodnoty polomeru gule, pričom polomer zakaždým zmeníte o malú hodnotu.

Existuje niekoľko spôsobov, ako vybrať polomer gule. Ak je vzdialenosť medzi th a th objektom, potom vyberte ako spodnú hranicu polomeru () a hornú hranicu polomeru možno definovať ako .

Ak spustíte algoritmus s hodnotou a zmeníte ju o malú hodnotu pri každom opakovaní, môžete identifikovať hodnoty polomerov, ktoré vedú k vytvoreniu rovnakého počtu zhlukov, t.j. na stabilný oddiel.

Príklad 1. Na základe údajov v tabuľke 1.1 je potrebné klasifikovať päť podnikov pomocou hierarchickej aglomeratívnej klastrovej analýzy.

Tabuľka 1.1

Tu: – priemerné ročné náklady na fixné výrobné aktíva, miliardy rubľov; – materiálové náklady na rubeľ vyrobených výrobkov, kopecks; – objem vyrobených produktov, miliardy rubľov.

Riešenie. Pred výpočtom matice vzdialenosti normalizujeme pôvodné údaje pomocou vzorca

Matica hodnôt normalizovaných premenných bude vyzerať

Klasifikáciu vykonáme pomocou hierarchickej aglomeračnej metódy. Na zostrojenie matice vzdialenosti použijeme euklidovskú vzdialenosť. Potom bude napríklad vzdialenosť medzi prvým a druhým objektom

Matica vzdialeností charakterizuje vzdialenosti medzi objektmi, z ktorých každý v prvom kroku predstavuje samostatný zhluk

Ako je zrejmé z matice, najbližšie objekty sú a. Spojme ich do jedného zhluku a priraďme mu číslo. Prepočítajme vzdialenosti všetkých zostávajúcich objektov (zhlukov) od zhluku a získajme novú maticu vzdialeností

V matici sú vzdialenosti medzi klastrami určené pomocou algoritmu „ďalekého suseda“. Potom je vzdialenosť medzi objektom a zhlukom

V matici opäť nájdeme najbližšie zhluky. Toto budú a , . Preto v tomto kroku kombinujeme aj klastre; dostaneme nový klaster obsahujúci objekty , . Dajme tomu číslo. Teraz máme tri zhluky (1,3), (2,5), (4).

Súdiac podľa matice, v ďalšom kroku spojíme zhluky a do jedného zhluku a priradíme mu číslo. Teraz máme iba dva klastre:

A nakoniec, v poslednom kroku spojíme zhluky vo vzdialenosti 3,861.

Uveďme výsledky klasifikácie vo forme dendrogramu (obrázok 1.5). Dendrogram naznačuje, že zhluk je homogénnejší v zložení prichádzajúcich objektov, pretože v ňom došlo k spojeniu na kratšie vzdialenosti ako v zhluku.

Obrázok 3.5: Dendrogram zhlukovania piatich objektov

Príklad 2. Na základe údajov uvedených nižšie klasifikujte predajne podľa troch kritérií: – predajná plocha, m2, – obrat na predajcu, deň. jednotky, – úroveň ziskovosti, %.

Číslo predajne				Číslo predajne

Na klasifikáciu obchodov použite metódu vyhľadávania klastrov (musíte vybrať prvý klaster).

Riešenie. 1. Vypočítajte vzdialenosti medzi objektmi pomocou euklidovskej metriky

kde , sú štandardizované hodnoty počiatočných premenných pre th a th objekt; t – počet vlastností.

2. Na základe matice Z vypočítame štvorcovú symetrickú maticu vzdialeností medzi objektmi ().

Analýza matice vzdialenosti pomáha určiť polohu počiatočného stredu gule a vybrať polomer gule.

V tomto príklade je väčšina „malých“ vzdialeností v prvom riadku, t.j. prvý objekt má pomerne veľa „blízkych“ susedov. Preto prvý objekt možno považovať za stred gule.

3. Nastavte polomer gule. V tomto prípade objekty, ktorých vzdialenosť od prvého objektu je menšia ako 2, spadajú do gule.

Jednou z iteratívnych klasifikačných metód, ktoré nevyžadujú špecifikáciu počtu zhlukov, je metóda vyhľadávania zhlukov. Metóda vyžaduje výpočet matice vzdialenosti a potom výber objektu, ktorý je počiatočným stredom prvého klastra. Výber takéhoto objektu môže byť ľubovoľný, alebo môže byť založený na predbežnej analýze bodov a ich okolia.

Vybraný bod sa berie ako stred hypersféry daného polomeru R. Určí sa množina bodov spadajúcich do tejto gule a vypočítajú sa pre ne súradnice stredu (vektor priemerných hodnôt vlastností). Ďalej sa uvažuje o hyperguli s rovnakým polomerom, ale s novým stredom, a pre množinu bodov, ktoré do nej spadajú, sa opäť vypočíta vektor priemerných hodnôt, ktorý sa považuje za nový stred gule, a tak ďalej. Keď ďalší prepočet súradníc stredu gule vedie k rovnakému výsledku ako v predchádzajúcom kroku, pohyb gule sa zastaví a body, ktoré do nej spadajú, vytvoria zhluk a sú vylúčené z ďalšieho procesu zhlukovania. Pre všetky zostávajúce body sa postupy opakujú.

Existuje teda viac nehierarchických metód, hoci fungujú na rovnakých princípoch. V podstate ide o iteratívne metódy fragmentácie pôvodnej populácie. Počas procesu delenia sa vytvárajú nové zhluky a tak ďalej, kým nie je splnené pravidlo zastavenia. Metódy sa medzi sebou líšia výberom počiatočného bodu, pravidlami pre vytváranie nových zhlukov a pravidlom zastavenia. Najčastejšie používaný algoritmus K-znamená.

Záver

Klastrová analýza je metóda zoskupovania objektov do tried na základe experimentálnych údajov o vlastnostiach objektov.

V tomto prípade sa používa klastrový model na reprezentáciu objektov - objekty s podobnými vlastnosťami patria do rovnakej triedy.

Zhluková analýza zahŕňa súbor rôznych klasifikačných algoritmov (príkladom metódy zhlukovej analýzy je metóda dendrogramu).

V tomto prípade sa počet tried a princípy rozdelenia do tried spravidla určujú vopred na základe všeobecných informácií o súbore objektov a cieľoch zhlukovej analýzy.

Metódy klastrovej analýzy sú doplnené metódami diskriminačnej analýzy, ktoré umožňujú určiť hranice medzi klastrami a použiť ich na riešenie problémov analýzy a klasifikácie dát.

Výsledky zhlukovej analýzy sú najčastejšie prezentované graficky vo forme dendrogramu („stromu“), zobrazujúceho poradie spájania objektov do zhlukov. Interpretácia štruktúry zhlukov, ktorá v mnohých prípadoch začína určením počtu zhlukov, je kreatívna úloha. Na to, aby to bolo efektívne vyriešené, musí mať výskumník dostatok informácií o objektoch, ktoré sú zoskupené. Pri kontrolovanom zhlukovaní môžu byť výsledky prezentované vo forme zoznamov objektov priradených každej triede.

Hlavnými výhodami zhlukovej analýzy sú absencia obmedzení na distribúciu premenných použitých v analýze; možnosť klasifikácie (klastrovania) aj v prípadoch, keď neexistujú a priori informácie o počte a charaktere tried; univerzálnosť (zhluková analýza môže byť aplikovaná nielen na kolekcie objektov, ale aj na súbory premenných alebo akékoľvek iné jednotky analýzy).

Uveďme si nevýhody klastrovej analýzy:

Podobne ako faktorová analýza môže vytvárať nestabilné zhluky. Opakujte štúdiu na iných ľuďoch a porovnajte výsledky klasifikácie. S najväčšou pravdepodobnosťou budú iné. Koľko je otázkou kvality samotného výskumu.

Implementuje induktívnu výskumnú metódu od konkrétneho k všeobecnému, ktorá je plná protivedeckých záverov. V ideálnom prípade by vzorka na klasifikáciu mala byť veľmi veľká, heterogénna, najlepšie vybraná stratifikáciou alebo randomizáciou. Veda sa uberá cestou testovania hypotéz, takže nie je potrebné preháňať zhlukovú analýzu. Najlepšie je použiť ho na testovanie hypotézy o prítomnosti akýchkoľvek typov, než vytvárať klasifikáciu od začiatku.

Ako každá metóda viacrozmerného škálovania, zhluková analýza má mnoho funkcií spojených s internými metódami. Aké je kritérium pre zoskupovanie ľudí do zhlukov, metóda hľadania rozdielov, počet krokov do dokončenia algoritmu v metóde k-means atď. preto sa výsledky môžu líšiť, aj keď nevýznamne, v závislosti od „nastavení“ postupu.

Existujú dve skupiny metód zhluková analýza: hierarchické a nehierarchické.

Hlavnými metódami hierarchickej klastrovej analýzy sú metóda najbližšieho suseda, metóda úplného spojenia, metóda priemerného spojenia a Wardova metóda. Posledná je najuniverzálnejšia.

Existuje viac nehierarchických metód, aj keď fungujú na rovnakých princípoch. V podstate ide o iteratívne metódy fragmentácie pôvodnej populácie. Počas procesu delenia sa vytvárajú nové zhluky a tak ďalej, kým nie je splnené pravidlo zastavenia. Metódy sa medzi sebou líšia výberom počiatočného bodu, pravidlami pre vytváranie nových zhlukov a pravidlom zastavenia. Najčastejšie používaný algoritmus K-znamená. Znamená to, že analytik vopred stanoví počet klastrov vo výslednom oddiele.

Keď už hovoríme o výbere konkrétnej metódy klastrovania, ešte raz zdôrazňujeme, že tento proces vyžaduje, aby analytik dobre poznal povahu a predpoklady metód, inak budú získané výsledky podobné „priemernej teplote v nemocnici“. Aby bola zvolená metóda skutočne účinná v danej oblasti, spravidla sa používa nasledujúci postup:

Zvažuje sa niekoľko a priori odlišných skupín a ich zástupcovia sa náhodne zmiešajú. Potom sa vykoná postup zhlukovania, aby sa obnovilo pôvodné rozdelenie do skupín. Ukazovateľom účinnosti metódy bude podiel zhôd medzi objektmi v identifikovanej a počiatočnej skupine.

Pri výbere medzi hierarchickými a nehierarchickými metódami by ste mali venovať pozornosť nasledujúcim bodom:

Nehierarchické metódy vykazujú vyššiu odolnosť voči odľahlým hodnotám, nesprávny výber metrík, zahrnutie nevýznamných premenných do základu pre zhlukovanie atď. Cenou za to je však slovo „a priori“. Výskumník musí vopred zaznamenať výsledný počet zhlukov, pravidlo zastavenia a, ak je to opodstatnené, počiatočné centrum zhlukov. Posledný bod výrazne ovplyvňuje účinnosť algoritmu. Ak nie je dôvod túto podmienku umelo nastavovať, vo všeobecnosti sa odporúča použiť hierarchické metódy. Všimnime si ešte jeden bod, ktorý je podstatný pre obe skupiny algoritmov: zoskupovanie všetkých pozorovaní nie je vždy tým správnym riešením. Môže byť opatrnejšie najprv vyčistiť vzorku od odľahlých hodnôt a potom pokračovať v analýze. Je tiež možné nenastaviť veľmi vysoké kritérium zastavenia.

Klastrová analýza je štatistická analýza, ktorá umožňuje rozdeliť veľké množstvo údajov do tried alebo skupín (z angličtiny, zhluk- trieda) podľa nejakého kritéria alebo ich kombinácie.

Vykonávať klasifikáciu údajov X x,...,X str použite pojem metriky alebo vzdialenosti.

Metrica je funkcia p, ktorá mapuje určitý metrický priestor do priestoru reálnych čísel a má tieto vlastnosti (metrické axiómy):

1) p(ZD>0,
2) p(X,Y)=p(Y,X),
3) p(X, Y) = 0 X = Y,
4) P(X,Y) P(Z,Y).

Teória zhlukovej analýzy používa na meranie vzdialenosti medzi jednotlivými bodmi (vektormi) nasledujúce metriky:

1) Euklidovská vzdialenosť

2) vážená euklidovská vzdialenosť

Kde w k - váhy úmerné dôležitosti vlastnosti v klasifikačnom probléme. Váhy sú stanovené po dodatočnom výskume

a predpokladajme, že ^w* = 1;

3) Hammingova vzdialenosť (alebo mestský blok) - vzdialenosť na mape medzi blokmi v meste

4) Mahalanobisova vzdialenosť (alebo Mahalanobisov uhol)

kde A je symetrická kladne definitná matica váhových koeficientov (často volená diagonálna); A - vektorová kovariančná matica X19...,Xp;

5) Minkowského vzdialenosť

Vzdialenosti 1), 2), 3) alebo 5) sa používajú v prípade normálneho rozdelenia nezávislých náhodných premenných X l9 ...,X n ~N(M,A) alebo v prípade ich homogénnosti v geochemickom význame, keď je každý vektor pre klasifikáciu rovnako dôležitý. Vzdialenosť 4) sa používa v prípade kovariančného vzťahu medzi vektormi X x,...,X P.

Výber metriky robí výskumník v závislosti od toho, aký výsledok chce získať. Tento výber nie je formalizovateľný, pretože závisí od mnohých faktorov, najmä od očakávaného výsledku, od skúseností výskumníka, úrovne jeho matematického vzdelania atď.

V mnohých algoritmoch sa spolu so vzdialenosťami medzi vektormi používajú aj vzdialenosti medzi klastrami a zväzky klastrov.

Nechaj S (- /tý klaster pozostávajúci z n t vektory alebo body. Nechaj

X (l) - vzorový priemer bodov spadajúcich do zhluku S f, alebo ťažisko klastra 5.. Potom sa rozlišujú nasledujúce vzdialenosti medzi klastrami, ktoré vo vnútri nemajú iné zhluky:

1) vzdialenosť medzi klastrami na základe princípu „najbližší sused“.

2) vzdialenosť medzi klastrami podľa princípu „vzdialeného suseda“.

3) vzdialenosť medzi ťažiskami skupín

4) vzdialenosť medzi klastrami podľa princípu „priemerného spojenia“.

5) zovšeobecnená Kolmogorovova vzdialenosť

Vzdialenosť medzi klastrami, ktoré sú zväzkami iných tried, možno vypočítať pomocou všeobecného vzorca:

Kde S^k^- zhluk získaný spojením tried S k A S t .

Všetky špeciálne prípady vzdialeností sú získané z tohto všeobecného vzorca. Pre a = p = 1/2, 8 = -1/2, y = 0 máme vzdialenosť podľa princípu „najbližší sused“, pre a = p = 5 = 1/2, y = O - „vzdialený sused“ “,

keď a =---, p =---,5 = 0, y = 0 - vzdialenosť pozdĺž ťažísk

p k + n i p k + n i

sti skupiny.

Metódy klastrovej analýzy sa delia na I) aglomeratívne (zjednocujúce), II) divízne (rozdeľujúce) a III) iteračné.

Prvé postupne spájajú jednotlivé objekty do zhlukov, tie druhé naopak zhluky rozdeľujú na objekty. Tretia kombinuje prvé dve. Ich vlastnosťou je vytváranie zhlukov na základe podmienok rozdelenia (tzv. parametrov), ktoré je možné počas prevádzky algoritmu meniť, aby sa zlepšila kvalita rozdelenia. Na klasifikáciu veľkého množstva informácií sa bežne používajú iteračné metódy.

Pozrime sa bližšie na aglomeratívne metódy. Aglomeratívne metódy sú najjednoduchšie a najbežnejšie medzi algoritmami klastrovej analýzy. V prvom kroku každý vektor alebo objekt X 19...,X s zdrojové údaje sa považujú za samostatný klaster alebo triedu. Na základe vypočítanej matice vzdialeností sa vyberú a skombinujú tie, ktoré sú najbližšie k sebe. Je zrejmé, že proces sa skončí (P - 1) krok, keď sa v dôsledku toho všetky objekty spoja do jedného zhluku.

Postupnosť asociácií môže byť reprezentovaná ako dendrogram alebo strom. Na obr. Obrázok 1.18 ukazuje, že v prvom kroku boli vektory kombinované Xt,X2, pretože vzdialenosť medzi nimi je 0,3.

V druhom kroku sa k nim pripojil vektor X 3, vzdialený od zhluku (X 1, X 2) vo vzdialenosti 0,5 atď. V poslednom kroku sa všetky vektory spoja do jedného zhluku.

Ryža. 1.18.

Aglomeratívne metódy zahŕňajú jednoduché, stredné, úplné spojenie a Wardovu metódu.

1.Jediný spôsob pripojenia. Nechaj Xv...,Xn - vektorové dáta, pričom každý vektor tvorí jeden zhluk. Najprv sa vypočíta matica vzdialeností medzi týmito klastrami, pričom sa ako metrika použije vzdialenosť najbližšieho suseda. Pomocou tejto matice sa vyberú dva najbližšie vektory, ktoré tvoria prvý zhluk 5,. Ďalší krok medzi S ] a zvyšných vektorov (ktoré považujeme za klastre), vypočíta sa nová matica vzdialenosti a vzdialenosť medzi zhlukmi zlúčenými do tried sa použije ako metrika (a = p = 1/2, 5 = -1/2, y = 0). Najbližšie k predtým získanej triede S ( zhluk s ním splýva, tvorí sa S 2. Atď. Cez P- 1 krok dostaneme, že všetky vektory sa spoja do jedného zhluku.

Výhody: 1) v každom kroku algoritmu sa pridáva iba jeden prvok, 2) metóda je extrémne jednoduchá, 3) algoritmus je necitlivý na transformácie zdrojových dát (rotácia, posun, posun, natiahnutie).

Nedostatky: 1) je potrebné neustále prepočítavať maticu vzdialeností, 2) počet zhlukov je vopred známy a nedá sa znížiť

2. Úplný spôsob pripojenia. Metóda prakticky opakuje metódu single link, okrem toho, že k zahrnutiu nového objektu do zhluku dochádza vtedy a len vtedy, ak je vzdialenosť medzi objektmi (vektormi alebo zhlukami) menšia ako určité vopred určené číslo. Číslo určuje používateľ. Vzdialenosť sa počíta len podľa princípu „ďalekého suseda“ (to isté možno povedať o vzdialenosti medzi triedami zlúčenými do tried - iba princíp vzdialeného suseda s oc = p = 8 = 1/2, y = 0).
3.Priemerný spôsob pripojenia. Algoritmus vytvárania zhlukov sa zhoduje s algoritmom jednoduchého spojenia, avšak pri rozhodovaní o zahrnutí nového objektu do klastra sa výpočty vykonávajú podľa princípu priemerného spojenia. Rovnako ako v metóde úplného prepojenia sa všetky vypočítané vzdialenosti medzi klastrami porovnávajú s číslom zadaným používateľom. A ak je (vzdialenosť) menšia ako dané číslo, nový objekt je zahrnutý do starej triedy. Metóda priemerného prepojenia sa teda od metódy úplného prepojenia líši iba spôsobom výpočtu vzdialenosti medzi zhlukami.
4. metóda WARD. Nechaj X 19...,X s- dáta, pričom každý vektor tvorí jeden zhluk. Nájdeme maticu vzdialenosti pomocou nejakej metriky (napríklad vzdialenosť Mahalanobis) a použijeme ju na určenie zhlukov, ktoré sú najbližšie k sebe. Vypočítame súčet štvorcových odchýlok vektorov v rámci zhluku S k podľa vzorca:

Kde Komu -číslo klastra, ja- vektorové číslo v klastri, j- súradnicové číslo X t e U1 R, p do- počet vektorov v zhluku, X jk- vzorový priemer X i V S k. Rozsah V k charakterizuje odchýlky vektorov od seba v rámci zhluku (nov S k + S f alebo starý^). Kalkulácia V k by sa mali vykonávať pred a po zlúčení a je potrebné prejsť všetkými možnými možnosťami takýchto združení. Neskôr v klastri S k pridajú sa len tie vektory alebo zhluky, ktoré vedú k najmenšej zmene V k po zlúčení a v dôsledku toho sa bude nachádzať v minimálnej vzdialenosti od pôvodného zhluku S k.

Pozrime sa ďalej na iteračné metódy. Podstatou iteračných metód je, že zhlukovanie začína nastavením niektorých počiatočných podmienok. Napríklad je potrebné nastaviť počet výsledných zhlukov alebo nastaviť vzdialenosť, ktorá určuje koniec procesu tvorby zhlukov atď. Počiatočné podmienky sa vyberajú podľa výsledku, ktorý výskumník potrebuje. Zvyčajne sa však špecifikujú pomocou riešenia nájdeného niektorou z aglomeračných metód. Medzi iteračné metódy patrí metóda ^-means a metóda hľadania kondenzácií.

1. /r-znamená metóda. Nech sú vektory X l9 ..., X n e9F a je potrebné ich rozdeliť na Komu klastre. V kroku nula od P náhodne vyberte vektory Komu z nich, berúc do úvahy, že každý tvorí jeden zhluk. Získame množinu štandardných zhlukov,...,e[ 0) s váhami

čoj 0),...,X. a vypočítajte maticu vzdialeností medzi X. a normy e 1 (0),...,^ 0) podľa nejakej metriky, napríklad euklidovskej:

Na základe znalosti vypočítanej matice vzdialenosti, vektora X ( umiestnené v tomto štandarde, ktorého vzdialenosť je minimálna. Predpokladajme s istotou, že je to tak. Nahrádza sa novým, prepočítaným s prihliadnutím na pripojený bod, podľa vzorca

Okrem toho sa hmotnosť prepočítava:

Ak sú v matici dve alebo viac minimálnych vzdialeností, potom X t zahrnuté v klastri s najnižším sériovým číslom.

V ďalšom kroku sa zo zostávajúcich vektorov vyberie ďalší vektor a postup sa zopakuje. Teda prostredníctvom ( PC) kroky pre každého

štandardné e^~ k) hmotnosť sa zhoduje a postup zhlukovania sa ukončí. S veľkými P a malé Komu algoritmus rýchlo konverguje k stabilnému riešeniu, t. j. k riešeniu, v ktorom sa štandardy získané po prvej aplikácii algoritmu zhodujú v množstve a zložení so štandardmi zistenými pri opakovaní metódy. Algoritmický postup sa však vždy niekoľkokrát opakuje, pričom sa ako štandardné vektory (ako počiatočná aproximácia) použije rozdelenie získané v predchádzajúcich výpočtoch: predtým nájdené štandardy e[ p k e (2 p k) k) sú brané za e (x 0) 9 ... 9 e (k 0) 9 a algoritmický postup sa opakuje.

2. Metóda hľadania kondenzácií. Toto je nasledujúci iteračný algoritmus. Nevyžaduje a priori špecifikáciu počtu klastrov. V prvom kroku je matica vzdialeností medzi X X9 ... 9 X p eU1 r podľa nejakej metriky. Potom sa náhodne vyberie jeden vektor, ktorý bude pôsobiť ako stred prvého klastra. Toto je počiatočná aproximácia. Predpokladajme, že tento vektor leží v strede p-rozmernej gule s polomerom R, a tento polomer špecifikuje výskumník. Potom sa určia vektory X Si,... 9 X Sk , spadajúce do tejto gule a z nich sa vypočíta výber
- 1 Komu

pevné matematické očakávanie X = ~Y]X 5. Potom je stred gule znova

nosí sa v X a postup výpočtu sa zopakuje. Podmienkou ukončenia iteračného procesu je rovnosť vektorov priemerov X, našiel na T A (t+ 1) kroky. Prvky uväznené vo vnútri gule X 9 ... 9 X

zaradíme ich do jedného zhluku a vylúčime z ďalšieho výskumu. Pre zostávajúce body sa algoritmus opakuje. Algoritmus konverguje pre akúkoľvek voľbu počiatočnej aproximácie a akékoľvek množstvo počiatočných údajov. Na získanie stabilného oddielu (t. j. oddielu, v ktorom sa zhluky nájdené po prvej aplikácii algoritmu zhodujú počtom a zložením so zhlukmi nájdenými pri opakovaní metódy), sa odporúča algoritmický postup niekoľkokrát zopakovať. pre rôzne hodnoty polomeru gule R. Znakom stabilného oddielu bude vytvorenie rovnakého počtu zhlukov s rovnakým zložením.

Všimnite si, že problém klastrovania nemá jediné riešenie. V dôsledku toho je pomerne ťažké vymenovať všetky povolené oddiely údajov do tried a nie je to vždy možné. Na vyhodnotenie kvality rôznych metód zhlukovania sa zavádza koncept funkcionálu kvality partície, ktorý má minimálnu hodnotu na najlepšom (z pohľadu výskumníka) oddiele.

Nechaj X X9 ... 9 X p e U1 R - určitý súbor pozorovaní, ktorý je rozdelený do tried S = (S19 ... 9 Sk) 9 a Komu vopred známy. Potom majú hlavné funkcie kvality oddielu pre známy počet klastrov tvar:

1) Vážený súčet vnútrotriednych rozptylov

Kde a(1)- selektívne matematické očakávanie zhluku S l.

Funkčné Q((S) nám umožňuje vyhodnotiť stupeň homogenity všetkých zhlukov ako celku.

2) Súčet párových vzdialeností v rámci triedy medzi prvkami alebo

Kde n 1- počet prvkov v zhluku S { .

3) Zovšeobecnený vnútrotriedny rozptyl

Kde n j- počet prvkov v S., A; . - vzorová kovariančná matica pre Sj.

Funkcionál je aritmetický priemer zovšeobecnených vnútrotriednych rozptylov vypočítaných pre každý klaster. Ako je známe, zovšeobecnený rozptyl umožňuje odhadnúť stupeň rozptylu viacrozmerných pozorovaní. Preto 3. otázka (S) umožňuje odhadnúť priemerné rozšírenie pozorovacích vektorov v triedach S l9 ... 9 S k . Odtiaľ pochádza jeho názov – zovšeobecnený vnútrotriedny rozptyl. 3. otázka (S) sa používa, keď je potrebné vyriešiť problém kompresie dát alebo koncentrácie pozorovaní v priestore s rozmerom menším ako bol pôvodný.

4) Kvalitu klasifikácie pozorovaní je možné posúdiť aj pomocou Hotellingovho kritéria. Aby sme to dosiahli, použijeme kritérium na testovanie hypotézy H 0 o rovnosti vektorov priemerov dvoch viacrozmerných populácií a vypočítajte štatistiku

Kde n t A p t - počet vektorov v triedach Sl,Sm; X, X t- centrované zdrojové údaje; S* - združená klastrová kovariančná matica S n S m: S* =--- (XjX l +X^X m). Ako predtým, hodnota Q 4 (S)

p,+p t-2

v porovnaní s tabuľkovou hodnotou vypočítanou podľa vzorca

Kde m- počiatočný rozmer pozorovacích vektorov a je hladinou významnosti.

Hypotéza H 0 je akceptovaná s pravdepodobnosťou (1-os), ak Q4(S)n_m, a je odmietnutý inak.

Kvalitu rozdelenia do tried možno posúdiť aj empiricky. Môžete napríklad porovnať priemer vzorky nájdený pre každú triedu s priemerom vzorky celej populácie pozorovaní. Ak sa líšia o faktor dva alebo viac, potom je rozdelenie dobré. Správnejšie porovnanie priemeru zhlukovej vzorky s priemerom vzorky celého súboru pozorovaní vedie k použitiu analýzy rozptylu na posúdenie kvality rozdelenia do tried.

Ak počet zhlukov v S = (Sl9 ...,Sk) je vopred neznámy, potom sa pre ľubovoľne zvolené celé číslo použijú nasledujúce funkcionály kvality partície m:

jajaKomu 1 1 m

- - priemerná miera v rámci triedy -

P i=1 n i XjeSj X"tSj J

rozhadzovanie sovy,

(1 P/ 1 W
- X ~-~ r “ miera koncentrácie bodov množiny

P nV l J J

S, - počet prvkov v zhluku obsahujúcom bod X g

Všimnite si, že pre ľubovoľnú hodnotu parametra T funkčné Zm(S) dosiahne minimum rovné I/p, ak počiatočné zhlukovanie S = (Sl9 ...,Sk) je rozdelenie do mono klastrov S. = (Xj), pretože V(Xt) = 1. V rovnakom čase Zm(S) dosiahne maximálne 1 ak S- jeden klaster obsahujúci všetky pôvodné údaje,

pretože V(X() = n. V špeciálnych prípadoch sa to dá ukázať Z_l(S)=-, Kde Komu - počet rôznych zhlukov v S = (Si9...9Sk)9ZX(S)= max - ,

*"V P)

Kde n t - počet prvkov v klastri S i9 Z^(S) = min - ,

G" P)

Všimnite si, že v prípade neznámeho počtu klastrov funguje kvalita oddielu Q(S) možno zvoliť vo forme algebraickej kombinácie (súčet, rozdiel, súčin, pomer) dvoch funkcionalít I m (S), Z m (S), keďže prvá je klesajúca a druhá rastúca funkcia počtu tried Komu. Takéto správanie Zm(S)

garantuje existenciu extrému Q(S).

Pri veľkom počte pozorovaní nie sú vhodné hierarchické metódy zhlukovej analýzy. V takýchto prípadoch sa používajú nehierarchické metódy založené na delení, ktoré sú iteračné metódy fragmentácia pôvodného obyvateľstva. Počas procesu delenia sa vytvárajú nové zhluky až do pravidlo zastavenia.

algoritmus k-means

Najčastejšie medzi nehierarchickými metódami algoritmus k-means, tiež nazývaný rýchla zhluková analýza. Kompletný popis algoritmu možno nájsť v Hartigan a Wong (1978). Na rozdiel od hierarchických metód, ktoré nevyžadujú predbežné predpoklady o počte zhlukov, aby bolo možné túto metódu použiť, je potrebné mať hypotézu o najpravdepodobnejšom počte zhlukov.

algoritmus k-means vytvára k zhlukov umiestnených v čo najväčšej vzdialenosti od seba. Hlavný typ problémov, ktoré rieši algoritmus k-means, - prítomnosť predpokladov (hypotéz) týkajúcich sa počtu zhlukov, ktoré by sa mali čo najviac líšiť. Výber k môže byť založený na predchádzajúcom výskume, teoretických úvahách alebo intuícii.

Všeobecná myšlienka algoritmu: daný pevný počet k pozorovacích zhlukov sa porovnáva so zhlukmi tak, aby sa priemery v klastri (pre všetky premenné) od seba čo najviac líšili.

Popis algoritmu

Počiatočná distribúcia objektov do zhlukov.
Vyberie sa číslo k av prvom kroku sa tieto body považujú za „stredy“ zhlukov. Každý zhluk zodpovedá jednému centru.

Výber počiatočných ťažísk možno vykonať nasledovne:
- výber k-pozorovaní na maximalizáciu počiatočnej vzdialenosti;
- náhodný výber k-pozorovaní;
- výber prvých k-pozorovaní.
Výsledkom je, že každý objekt je priradený ku konkrétnemu zhluku.
Iteračný proces.
Vypočítané klastrové centrá, ktoré sa potom a ďalej považujú za súradnicové priemery zhlukov. Objekty sa opäť prerozdelia.

Proces výpočtu centier a prerozdeľovania objektov pokračuje, kým nie je splnená jedna z podmienok:
- klastrové centrá sa stabilizovali, t.j. všetky pozorovania patria do klastra, do ktorého patrili pred aktuálnou iteráciou;
- počet iterácií sa rovná maximálnemu počtu iterácií.
Na obr. 14.1 ukazuje príklad činnosti algoritmus k-means pre k rovné dvom.

Ryža. 14.1.

Výber počtu klastrov je zložitý problém. Ak neexistujú žiadne predpoklady týkajúce sa tohto počtu, odporúča sa vytvoriť 2 zhluky, potom 3, 4, 5 atď., Porovnaním získaných výsledkov.

algoritmus môže byť pomalý vo veľkých databázach. Možným riešením tohto problému je použitie vzorkovania údajov.

Typy postupov zhlukovej analýzy. I.A

Záver

algoritmus k-means

Popis algoritmu